2015-04-12
2373
Каноническое уравнение эллипса.
Теорема. В канонической для эллипса системе координат уравнение эллипса имеет вид:
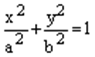. (4)
Доказательство. Доказательство проведем в два этапа. На первом этапе мы докажем, что координаты любой точки, лежащей на эллипсе удовлетворяют уравнению (4). На втором этапе мы докажем, что любое решение уравнения (4) дает координаты точки, лежащей на эллипсе. Отсюда будет следовать, что уравнению (4) удовлетворяют те и только те точки координатной плоскости, которые лежат на эллипсе. Отсюда и из определения уравнения кривой будет следовать, что уравнение (4) является уравнением эллипса.
1) Пусть точка М(х, у) является точкой эллипса, т.е. сумма ее фокальных радиусов равна 2а:
.
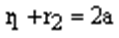Воспользуемся формулой расстояния между двумя точками накоординатной плоскости и найдем по этой формуле фокальные радиусы данной точки М:
, 
,
.
.
.
,
.
.
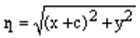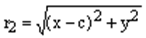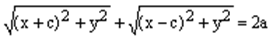
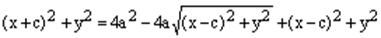
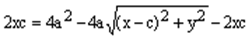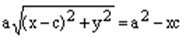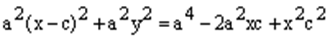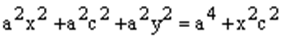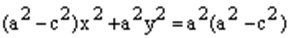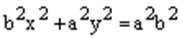Разделив последнее равенство на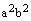 
, получаем равенство (4), ч.т.д.
Определение. Уравнение (4) называется каноническим уравнением эллипса. Канонические для эллипса оси координат называются главными осями эллипса. Начало канонической для эллипса системы координат называется центром эллипса. Директрисами эллипса называются две прямые, которые в канонической для эллипса системе координат имеют уравнения
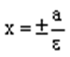или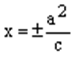 
. (13)
Теорема. Пусть М – произвольная точка эллипса,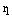 
, 
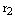– ее фокальные радиусы, 
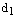– расстояние от точки М до левой директрисы, 
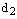– до правой. Тогда
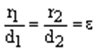, (14) где 
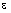– эксцентриситет эллипса.
