Способы задания прямой
Векторно-параметрическое уравнение прямой 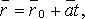
где 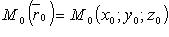 - фиксированная точка, лежащая на прямой;
- фиксированная точка, лежащая на прямой; 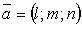 - направляющий вектор.
- направляющий вектор.
В координатах (параметрические уравнения): 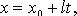
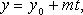
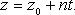
Канонические уравнения прямой
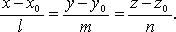
Уравнения прямой по двум точкам
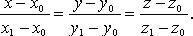
Прямая как линия пересечения двух плоскостей
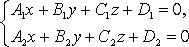
при условии, что не имеют места равенства
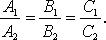
Взаимное расположение двух прямых
Если прямые заданы уравнениями 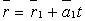 и
и 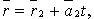 то они:
то они:
1) параллельны (но не совпадают) 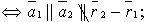
2) совпадают 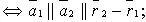
3) пересекаются 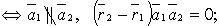
4) скрещиваются 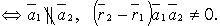
Угол между прямыми. Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.
Пусть в пространстве заданы две прямые:
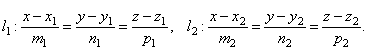
Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами 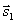 и
и 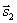 . Так как
. Так как 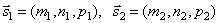 , то по формуле для косинуса угла между векторами получим
, то по формуле для косинуса угла между векторами получим
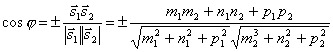 .
.
Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов 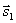 и
и 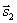 : Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l1 параллельна l2 тогда и только тогда, когда
: Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l1 параллельна l2 тогда и только тогда, когда 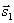 параллелен
параллелен 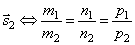 .
.
Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю: 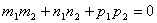 .
.
 2015-04-12
2015-04-12 1679
1679
