Контрольные работы. Контрольные работы по начертательной геометрии представляют собой эпюры (чертежи), которые выполняются по мере последовательного прохождения курса

Контрольные работы по начертательной геометрии представляют собой эпюры (чертежи), которые выполняются по мере последовательного прохождения курса. Каждый контрольный эпюр сопровождается планом его решения, т.е. кратким описанием хода решения задачи.

Каждая контрольная работа представляется на рецензию в полном объеме (необходимое число эпюров с объяснительными записками к ним). Представление контрольных работ по частям (с отдельными эпюрами) не разрешается. На каждую контрольную работу преподаватель кафедры составляет рецензию, в которой кратко отмечает достоинства и недостатки работы. Контрольную работу вместе с рецензией возвращают студенту, и она храниться у него до зачета.

Пометки преподавателя на чертежах стирать нельзя. Все замечания и указания преподавателя должны быть приняты студентом к исполнению. Если работы не зачтены, преподаватель в рецензии указывает, какую часть контрольной работы нужно переделать или же выполнить всю контрольную работу вновь. На повторную рецензию следует представлять всю контрольную работу полностью. К выполнению следующей контрольной работы нужно приступить, не ожидая ответа на предыдущую.

Контрольные работы представляются на рецензию строго в сроки, указанные в учебном графике. Эпюры контрольных работ выполняются на листах чертежной бумаги формата (210x297). На расстоянии 5 мм от линии обреза листа проводится рамка поля чертежа. С левой стороны линия рамки проводится от линии обреза листа на расстоянии 20 мм. Внизу формата вплотную к рамке помещается основная надпись.

Чертежи заданий вычерчиваются в заданном масштабе и размещаются с учетом наиболее плотного размещения всего эпюра в пределах формата листа.

Все надписи, как и отдельные обозначения в виде букв и цифр на эпюре, должны быть выполнены стандартным шрифтом размером 3,3 и 5 в соответствии с ГОСТ 2.304-68.

Эпюры выполняются с помощью чертежных инструментов: вначале карандашом с последующей обводкой всей основных построений тушью или пастой шариковой ручки. На тщательность построений должно быть обращено серьезное внимание. Небрежное выполнение построения не только снижают качество чертежа, но и приводят к неправильным результатам.

При обводке тушью (пастой) характер и толщина линий берутся в соответствии с ГОСТ 2.303-68. Все видимые основные линии сплошные толщиной S=0,8 - 1,0 мм. Линии центров и основные - штрихпунктирные толщиной от S/2 до S/3 мм. Линии построений и линии связи должны быть сплошными и наиболее тонкими. Линии невидимых контуров показывать штриховыми линиями. На это следует обратить внимание при выполнении всех контрольных работ, имея при этом в виду, что заданные плоскости и поверхности непрозрачны.

Желательно при обводке пользоваться цветной тушью (пастой). При этом все данные линии обводятся черной тушью (пастой), искомые линии - красной тушью (пастой), линии построений - синей или зеленой тушью (пастой). Все основные вспомогательные построения должны быть сохранены.

Точки на чертеже желательно вычерчивать в виде окружности диаметром 1,5 - 2,0 мм (см. чертежи - образцы в учебниках). Рекомендуется отдельные видимые элементы покрывать бледными тонами красок, используя акварель, разведенную в воде тушь, чай или цветные карандаши. Всегда, однако, следует помнить о том, чтобы тона были очень бледными, не затемняли линий построений, надписей и обозначений.

Каждый эпюр сопровождается пояснительной запиской, в которой на одном листе писчей бумаги формата (210x297) кратко излагаются план решения задачи и последовательность графических построений.

Учебно-тематический план

Тема	Количество часов
Лекции	Практ. занятия	Самост. занятия
Тема 1. Предмет начертательной геометрии. Точка
Тема 2. Прямая
Тема 3. Плоскость
Тема 4. Основные позиционные и метрические задачи
Тема 5. Способы преобразования чертежа
Тема 6. Поверхность
Тема 7. Пересечение плоскости и прямой с поверхностью
Тема 8. Пересечение поверхностей
Тема 9. Развертки поверхностей
Тема 10. Стандарт ECK D
Тема 11. Резьбы
Тема 12. Шероховатость поверхностей
Тема 13. Виды изделий
Всего
Итого

Учебные материалы

Тема 1. Предмет начертательной геометрии. Точка.

Начертательная геометрия является частью общей геометрии и изучает геометрические основы различных способов изображения пространственных форм и способов решения пространственных задач.

Не всякое изображение предмета позволяет точно определить его геометрическую форму. Для точного определения геометрии предмета необходимо, чтобы изображение выполнялось по определенным правилам. Такое изображение достигается при помощи метода проецирования, который является основным методом начертательной геометрии, а чертежи, выполненные по этому методу, называются проекционными.

Как всякая математическая дисциплина, начертательная геометрия должна изучаться в строгой последовательности. Все последующее логически вытекает из предыдущего. Например, не освоив проецирования точки, первого геометрического элемента, нельзя изучить проецирование прямой. Не зная проецирования прямой, нельзя перейти к плоскости и т.д.

Сама по себе теория начертательной геометрии достаточно проста. Основная трудность предмета заключается в применении этой теории к решению практических задач. Поэтому, только последовательно переходя от одного раздела к следующему, можно успешно освоить весь курс начертательной геометрии.

Курс начертательной геометрии нельзя просто читать. Необходимо, вооружившись карандашом и простейшим чертежным инструментом – циркулем, линейкой, на клетчатой бумаге воспроизвести все построения изложенные в курсе. Применение клетчатой бумаги позволяет вести построения точнее, не допуская ошибок. Хорошую ориентировку в построении дает применение цветных карандашей.

Для успешного изучения дисциплины важно твердое усвоение принятой терминологии, буквенных обозначений, типовых схем и т.д.

Из всего материала курса следует обратить внимание на расположение и взаимосвязь трех проекций точки. Эта схема является азбукой всей инженерной графики. От нее берет начало расположение трех основных проекций любого предмета, принятое во всех чертежах:

- главный вид – вертикальная фронтальная проекция точки.

- вид сверху – горизонтальная проекция.

- вид слева – профильная проекция.

Без абсолютно четкого понимания этой принципиальной схемы нельзя изучать теорию инженерной графики.

Очень важным является отчетливое понимание расположения осей и их знаков в совмещенном положении плоскостей. Для лучшего усвоения и понимания рекомендуется при составлении данной схемы обозначение осей и их знаки наносить полностью. И только когда наступит полная ясность и закрепится в памяти, можно перейти к сокращенному обозначению только положительных направлений.

СВОЙСТВА ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ

Геометрически закономерное изображение пространственных форм (фигур, линий, точек и т.д.) на плоскости достигается мето­дом проецирования, а чертежи, построенные по этому методу, назы­ваются проекционными.

В практике проецирования используются два способа:

1. Центральное проецирование.

2. Параллельное проецирование, как наиболее распространенное в инженерной графике.

Центральное проецирование

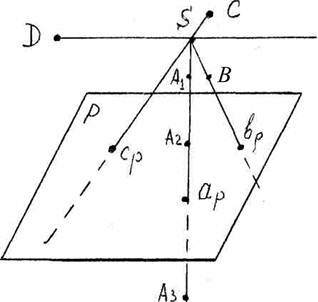Для получения центральных проекций (центральное проецирование) надо задаться плоскостью проекций и центром проекций - точкой, не лежащей в этой плоскости (Рис. 1: P - плоскость проекций; S - центр проекций - точка).

Рис. 1

Взяв некоторую точку А и проведя, через S и A₁ прямую линию до пересечения ее с плоскостью Р, получим точку а_р, Также поступаем, например, с точками В и С. Точки а_р, в_р, с_р являются цент­ральными проекциями точек A₁, В, С на плоскость Р: они получаются в пересечении проецирующих прямых (лучей) SA₁, SB, SС с плоскостью проекций Р.

Очевидно, если изменить центр проекций, то получатся новые проекции точек на плоскость Р.

На примере центрального проецирования основано фотографиро­вание, кинопроектирование и выполнение чертежей способом линейной перспективы. Линейная перспектива применяется в архитектуре.

Параллельное проецирование

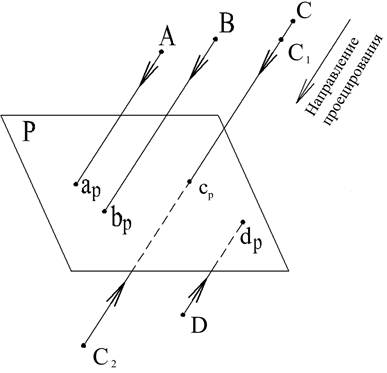При параллельном проецировании считается, что центр проек­ций отсутствует, а есть только направлении проецирования. При этом все проецирующие прямые (лучи) параллельны между собой и параллель­ны заданному направлению (рис. 2).

Рис. 2

Следовательно, параллельной проекцией точки будем называть точку пересечения проецирующей прямой, проведенной параллельно заданному направлению, с плоскостью проекций.

Рассмотрим свойства параллельного проецирования.

1. Каждой точке пространства соответствует одна проекция этой точки на плоскости проекций (рис. 2: А, В, С).

2. Одна проекция не определяет положение точек в пространстве (рис. 2: С C₁, С₂).

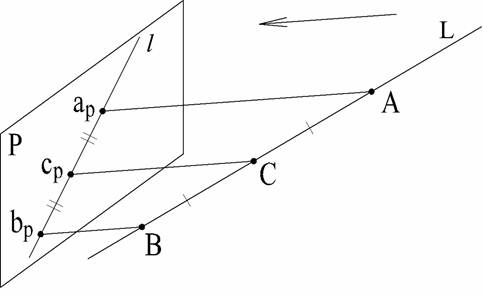3. Проекция прямой - есть прямая (рис. 3). Действительно, проецирующие лучи, проходящие через точки прямой L (рис. 3: А, В, С), образуют плоскость, которая пересе­кается с плоскостью проекций Р по линии l. Эта линия является проекцией прямой L.

Рис. 3

4. Если пространственный отрезок прямой АВ разделить в за­данном отношении (рис. 3 - отрезок АВ точкой С делится пополам), то и проекция этого отрезка а_р в_р разделится в том же отношении. Это очевидно, если вспомнить теорему о пропорциональности отрез­ков прямых между параллельными прямыми (параллельные проецирующие лучи).

5. Проекции параллельных линий параллельны между собой (ес­ли две параллельные плоскости пересечь третьей плоскостью, то ли­нии пересечения этих плоскостей будут параллельны).

6. Каждая линия на плоскости проекций может быть проекцией множества линий, если они расположены в общей для них проецирую­щей плоскости (рис. 4)

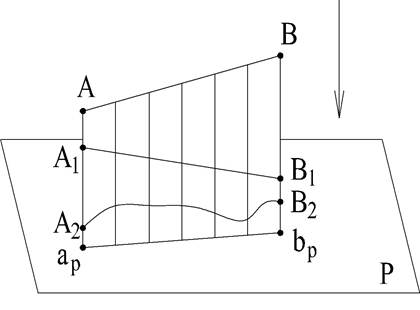
Рис. 4

Отрезок а_рв_р служит проекцией отрезков АВ, A₁B₁ и отрезка плоской кривой A₂B₂.

7. Для построения проекции прямой достаточно спроецировать две ее точки и через полученные проекции этих точек провести пря­мую линию.

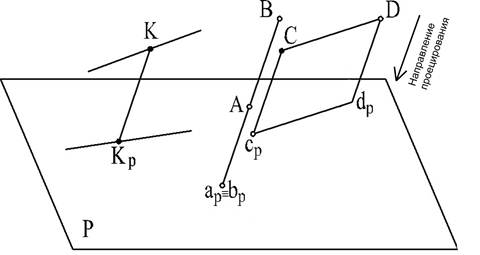8. Если точка принадлежит прямой, то проекция точки принад­лежит проекции этой прямой (рис. 5: точка К принадлежит прямой, к_р принадлежит проекции этой прямой).

Рис. 5

9. Если прямая параллельна направлению проецирования (рис.5 прямая АВ), то проекцией прямой (и любого ее отрезка) является точка (а_р совпадает с в_р).

10. Отрезок прямой линии, параллельной плоскости проекций, проецируется на эту плоскость в натуральную величину (рис. 5: CD = c_pd_p

как отрезки параллельных прямых).

Из рассмотренных свойств следуют два очень важных следствия:

1. Сохраняется пропорциональность изображения (проекции) и предмета в натуре.

2. Параллельность линий (ребер) в натуре сохраняется в изображении.

В начертательной геометрии и инженерной графике (техническом черчении) в основном применяется способ параллельного прямоуголь­ного проецирования, т.е. направление проецирования - проецирующие лучи перпендикулярны плоскости проекций. Этот способ называется ортогональным проецированием.

ПРОЕЦИРОВАНИЕ ТОЧКИ НА ТРИ ПЛОСКОСТИ ПРОЕКЦИЙ. МЕТОД МОНЖА.

Одним из свойств параллельного проецирования является то, что одна проекция не определяет положения точек в пространстве.

С развитием техники первостепенное значение приобрел вопрос о применении метода, обеспечивающего точность и удобоизмеримость изображений, т.е. возможность точно установить место каждой точки изображения относительно других точек или плоскостей и путем прос­тых приемов определить размеры отрезков линий и фигур.

Такой метод был предложен Гаспаром Монжем (Гаспар Монж -(1746 - 1818) французский ученый, математик-геометр, инженер, го­сударственный деятель в период революции 1789-1794 г.г. и правле­ния Наполеона Бонапарта).

Излож е нный Монж е м метод - метод параллельного проецирования (причем берутся прямоугольные проекции на две взаимно перпендику­лярные плоскости проекций) - был и остается основным методом сос­тавления технических чертежей.

Слово прямоугольный в литературе заменяют словом ортогональ­ный. При изучении начертательной геометрии термин ортогональные проекции применяется для обозначения системы прямоугольных проек­ций на взаимно перпендикулярных трех плоскостях.

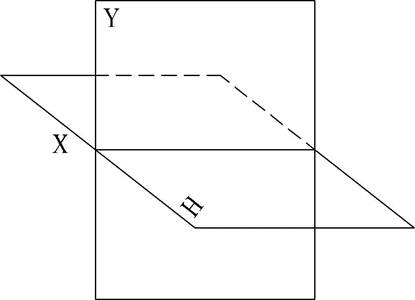Рис. 6

На рис. 6 изображены две взаимно перпендикулярные плоскости. Примем их за плоскости проекций и обозначим буквой Н плоскость расположенную горизонтально, а буквой V - вертикально. Вертикальную плоскость V принято называть фронтальной, а плоскость Н - горизонтальной плоскостью проекций. Они образуютсистему V, Н.

Линия пересечения плоскостей проекций называется осью проек ций. Осьпроекций разделяет каждую из плоскостей V и Н на полуплоскости (отсеки). Эта ось обозначается X или в виде дроби V/Н. Спроецируем на эти плоскости (рис. 7,а) некоторую пространственную точку А.

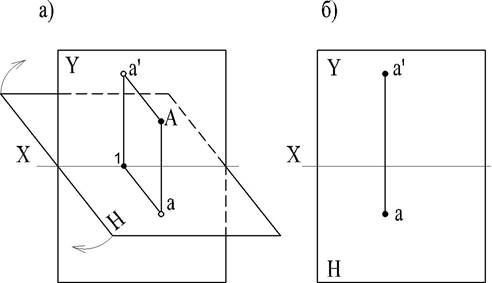Рис. 7

Проведя из точки А перпендикуляры к V и Н, получим проекции точки А:

фронтальную (вертикальную) на плоскость V, обозначенную а’

горизонтальную на плоскость Н, обозначенную а.

Проецирующие прямые соответственно, перпендикулярные к V и H, являются пересекающимися прямыми в точке А, следовательно они определяют плоскость, перпендикулярную к плоскостям проекций и к оси проекций X. Эта плоскость в пересечении с V и Н образует две взаимно перпендикулярные прямые а'1 и а1, пересекающиеся в точке 1 на оси проекций X. Следовательно проекции некоторой точки получаются расположенными на прямых, перпендикулярных к оси проекций и пересекающих эту ось в одной и той же точке.

Две проекции точки вполне определяют ее положение в пространстве относительно данной системы плоскостей проекций.

Для получения чертежа (рис. 7, б) плоскость Н поворачивают вокруг оси X, как показано на рис. 7а до совмещения с плос­костью V. В результате поворота образуется одна плоскость изоб­ражений, на которой точка показывается своими проекциями (а' и а).

Проекции а' и а расположатся на одном перпендикуляре к оси проекций. Этот перпендикуляр называется проекционной линией связи.

В результате такого совмещения плоскостей V и Н получается чертеж, известный под названием эпюр - эпюр Монжа (с французского Epure - проект, чертеж).

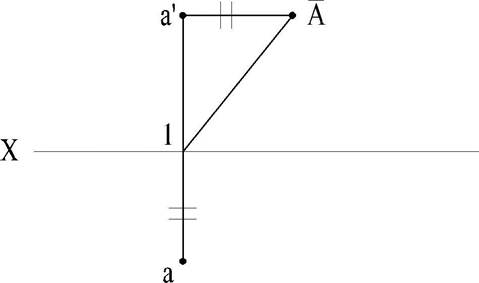Так как при наличии оси проекций положение точки А относи­тельно плоскостей проекций V и Н установлено, то отрезок а'1 вы­ражает расстояние точки А от плоскости Н, а отрезок al - расстоя­ние точки А от плоскости V. Отсюда можно определить расстояние точки А от оси проекций. Оно выражается гипотенузой треугольника, построенного по катетам а'1 и al (рис.8)

Рис. 8

Откладывая на чертеже отрезок а'А, равный A1, перпендикуляр­но к а'1, получаем гипотенузу A1, выражающую искомое расстояние.

Следует обратить внимание на необходимость проведения линий связи между проекциями точки.

Решение рассмотренной задачи было достигнуто с применением только двух взаимно перпендикулярных плоскостей проекций. Но в бо­лее общем виде проецирование ведется на три взаимно перпендикуляр­ные плоскости как отвечающие трем измерениям объемной формы, т.е. длине, ширине и высоте, также имеющих взаимно перпендикулярное по­ложение в пространстве.

Следует помнить, что число проекций и равное ему число плос­костей проекций во всех случаях должно выбираться минимальным, но достаточным для решения поставленной задачи.

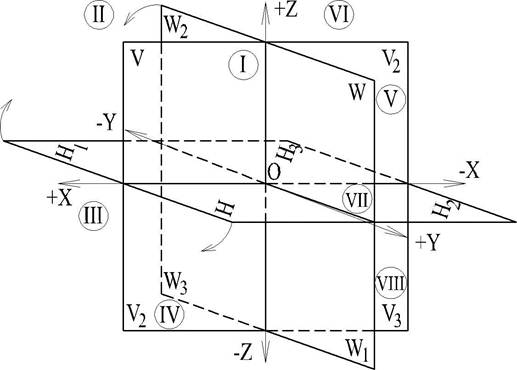В системе трех взаимно перпендикулярных плоскостей проекций (рис. 9) главной является вертикальная (фронтальная) плоскость V; второй - горизонтальная плоскость Н; третья, перпендикулярная к двум первым, называется профильной и обозначается буквой W. При своем пересечении эти плоскости образуют три взаимно перпендикуляр­ные прямые, называемые осями координат х, у, z; точка 0, точка их пересечения, называется началом координат.

Рис. 9

Оси координат х, у, zот начала координат 0 расположены в двух противоположных направлениях. Для обозначения этих направле­ний вводится правило знаков. Направление оси х влево принято счи­тать положительным (+х), а вправо - отрицательным (-х). Направле­ние оси у вперед считается положительным (+у), а назад - отрица­тельным (-у). Направление оси zвверх считается положительным (+Z), и вниз - отрицательным (-z).

Таким образом, пространство, в котором расположена система трех взаимно перпендикулярных плоскостей, делится на восемь частей называемых октантами. Основным считается первый октант.

Для совмещения всех трех плоскостей в одну способом условного поворота за основу принимается фронтальная (вертикальная) плоскость V, остающаяся в неизменном положении. Горизонтальная плоскость Н, вращаясь вокруг оси х, передним краем отсека опускается вниз; а профильная плоскость W, вращаясь вокруг вертикальной оси Z, передним краем отводится вправо.

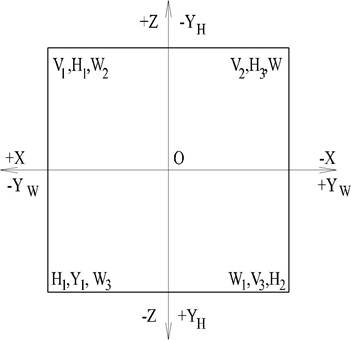Итак, ось у не является осью вращения отсеков плоскостей и принадлежит одновременно как плоскости Н: у_н (у), так и плоскости W: y_w(y₁) (рис. 10).

Рис. 10

Рассмотрим теперь точку в трех взаимно перпендикулярных плоскостях проекций.

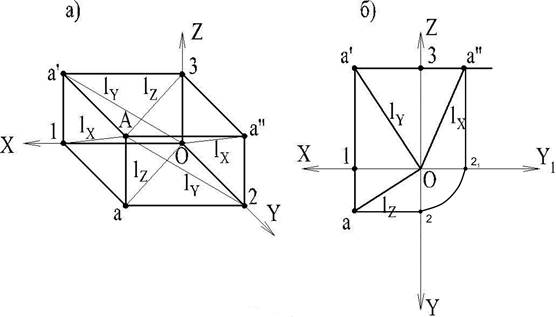Рис. 11

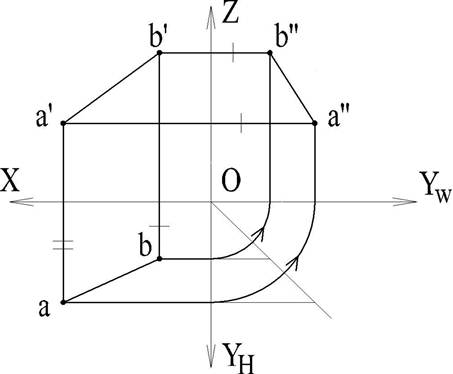
Наглядное изображение (рис. 11, а) и чертеж (рис. 11, б) содержат горизонтальную а, фронтальную а и профильную А проекции неко­торой точки А.

Горизонтальная и фронтальная проекции (а и а') расположены на одном перпендикуляре к оси X - на линии связи а' а; фронтальная и профильная проекции (а и а') - на одном перпендикуляре к оси Z - на линии связи а'а". Порядок построения профильной проек­ции точки а" по фронтальной а' и горизонтальной а представлен на рис. 11б.

Расстояние точки А от плоскости Н измеряется на чертеже (рис. 11, б) отрезком а' 1 или a" 2₁; расстояние от V- отрезком a1 или отрезком a"3;

расстояние от W - отрезком а2 или отрезком а'3.

Расстояние от точки А до оси X измеряется в пространстве отрезком A1 = lx. Аналогично расстояние от точки А до оси У выражается отрезком l_y и расстояние от точки А до оси z- от­резком l_z.

Таким образом, расстояния точки от плоскостей проекций и от осей проекций, могут быть измерены непосредственно, как определен­ные отрезки на чертеже (с учетом масштаба), т.е. модель положения точки в системе плоскостей проекций V, Н, W аналогична модели в системе декартовых координат.

Действительно, прямые, по которым пересекаются плоскости координат, называются осями координат. Точка пересечения осей координат обозначается буквой 0.

На рис. 11, а рассмотрим образование отрезков, определяющих координаты некоторой точки А: из точки А проведены перпендикуляры к каждой из плоскостей координат. Первая координата точки, называ­емая абсциссой, выразится числом, полученным от сравнения отрезка Аа" (или равного ему отрезка 01 на оси X) с некоторым отрезком, принятым за единицу масштаба. Также отрезок Аа' (или равный ему отрезок 02 на оси У) определит вторую координату точки А, называемую ординатой. Отрезок Аа (или равный ему отрезок 03 на оси Z) - третью координату, называемую аппликатой.

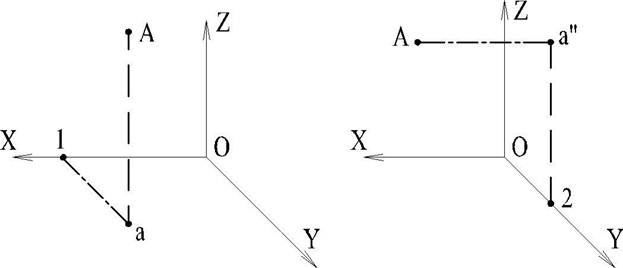Таким образом, построение точки по заданным ее координатам сводится к построению трех ребер параллелепипеда координат, сос­тавляющих трехзвенную ломаную линию (рис. 12)

Рис. 12

Например, надо отложить последовательно отрезки 01, 1а, аА или 02, 2а" и а"А и т.д., т.е. точку А при известных координатах можно построить шестью комбинациями, в каждой из которых должны быть все три координаты.

Следовательно, построение проекций точки сопровождается построением отрезков, определяющих координаты этой точки, если принять плоскости проекций за плоскости координат. Каждая из про­екций точки А определяется двумя координатами этой точки; например, положение проекции а определяется координатами х и у.

ТЕМА 2. ПРЯМАЯ

Прямая общего положения

Прямая, не параллельная никакой плоскости проекций и пред­ставляющая самый общий случай положения прямой в пространстве от­носительно принятой системы плоскостей проекций, называется прямой общего положения (рис. 13).

а) б б б)

Рис. 13

При любом способе проецирования прямой на плоскость проекция ее будет прямая линия.

Из элементарной геометрии известно, что две точки определяют положение прямой в пространстве. Отсюда проекции этих точек опре­деляют положение проекций линии.

Спроектируем точки А и В (рис. 13б) на фронтальную и гори­зонтальную плоскости проекций. Проведя через одноименные проекции этих точек прямые линии, мы получим проекции отрезка АВ:

фронтальную а' в' и

горизонтальную ав.

Чертеж отрезка АВ можно представить в системе трех плоскостей проекций: V, Н, W (рис. 14).

Рис. 14

Проекции а" в" могут быть построены любым из известных способов (главное - минимальное количество линий построения).

Прямые частного положения (Прямые уровня)

Прямая линия может занимать относительно плоскостей проекций (кроме общего положения) частные (особые) положения. Их целесооб­разно разделить на две группы:

1. Прямая параллельна одной из плоскостей проекций.

2. Прямая параллельна двум плоскостям проекций.

Прямая параллельна одной плоскости проекций

1. Прямая параллельна плоскости Н (рис. 15).

В таком случае фронтальная проекция прямой параллельна оси проекций х, а горизонтальная проекция отрезка этой прямой равна самому отрезку, т.е. ав = АВ. Такая прямая называется горизонталь­ной прямой или горизонталью.

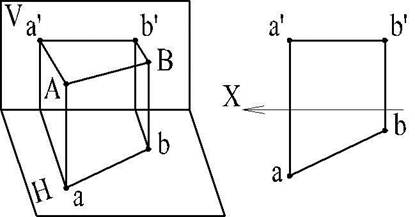Рис. 15

Если, например, проекция а' в' совпадает с осью проекций х, отрезок АВ расположен в плоскости Н.

2. Прямая параллельна плоскости V (рис. 16).

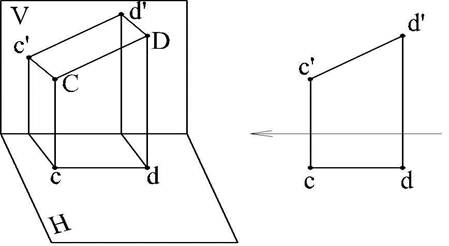
Рис. 16

B этом случае горизонтальная проекция прямой сd параллельна оси проекций, а фронтальная проекция отрезка этой прямой равна самому отрезку: c'd' = CD).

Такая прямая называется фронтальной прямой или фронталью.

Если, например, проекция сd совпадает с осью проекций, то это соответствует положению отрезка СD в самой плоскости V.

3. Прямая параллельна плоскости W (рис. 17).

В таком случае горизонтальная и фронтальная проекции прямой располагаются на одном перпендикуляре к оси проекций х, а профильная проекция этой прямой равна самому отрезку: e"f" = EF Такая прямая называется профильной прямой.

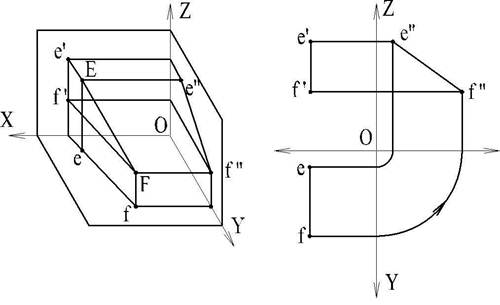Рис. 17

Прямая параллельна двум плоскостям проекций (Проецирующие прямые)

1. Прямая параллельна плоскостям V и W (рис. 18).

Если какая-либо прямая параллельна плоскостям V и W, тo она перпендикулярна к плоскости Н. Проекция прямой на плоскость W представляет собой отрезок параллельный и равный e' f'. Эта прямая называется горизонтально проецирующей прямой.

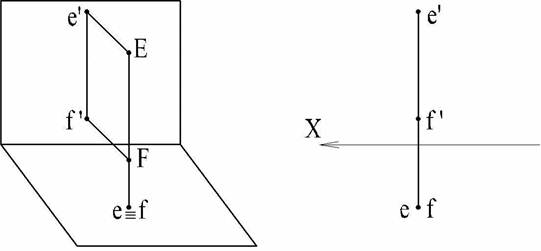Рис. 18

2. Прямая параллельна плоскостям Н и W (рис. 19)

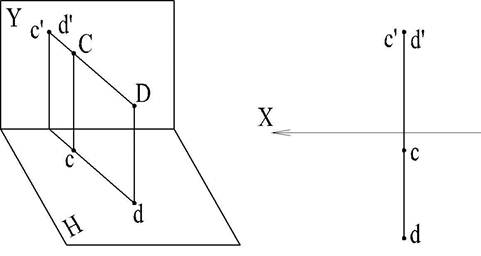Рис. 19

3. Прямая параллельна плоскостям V и Н (рис. 20)

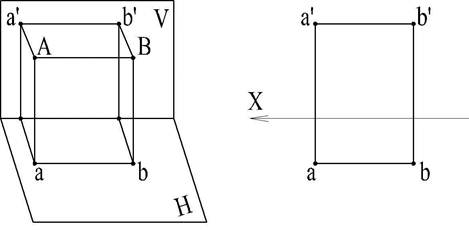Рис. 20

Если какая-либо прямая параллельна плоскостям V и Н, то она перпендикулярна к плоскости W. Проекция этой прямой на плоскость Wпредставляет собой точку, т.е. эта прямая является профильно проецирующей. Проекции отрезка прямой АВ на плоскости V и Н равны самому отрезку, т.е. отрезок прямой проецируется на эти плос­кости в натуральную величину.

Следы прямой

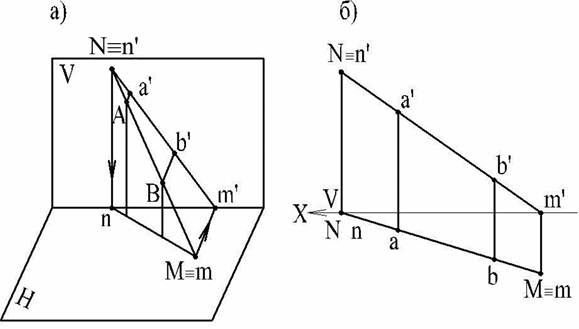Рис. 21

На рис. 21, а показаны точки М и N, в которых прямая, заданная отрезком АВ, пересекает плоскости проекций. Эти точки пере­сечения прямой с плоскостями проекций называются ее следами:

точка М - горизонтальный след прямой;

точка N - ее фронтальный след.

Горизонтальная проекция горизонтального следа (точка т) совпадает с самим следом М, а фронтальная проекция этого следа m' лежит на оси проекций.

Фронтальная проекция фронтального следа n' совпадает с точ­кой N, а горизонтальная проекция nлежит на той же оси проек­ций.

Следовательно, чтобы найти горизонтальный след, надо (рис. 21, б) продолжить фронтальную проекцию а'в' до пересечения с осью системы V/Н (ось х) и через точку m'(фронтальную проекцию го­ризонтального следа) провести перпендикуляр к оси х до пересечения с продолжением горизонтальной проекции ав. Точка пересечения m -есть горизонтальная проекция горизонтального следа; она совпадает с самим следом.

Для нахождения фронтального следа продолжаем горизонтальную проекцию ав до пересечения с осью х; через точку n(горизонталь­ную проекцию фронтального следа) проводим перпендикуляр до пересе­чения с продолжением фронтальной проекции а'в'. Точка n' - фронтальная проекция фронтального следа; она совпадает с самим сле­дом N.

По положению точек М и Nможно легко судить, к каким чет­вертям (октантам) пространства отнесена данная прямая.

ОПРЕДЕЛЕНИЕ НАТУРАЛЬНОЙ ВЕЛИЧИНЫ ОТРЕЗКА ПРЯМОЙ

Из рассмотренных свойств параллельного (ортогонального) проецирования известно, что отрезок прямой линии, параллельной плос­кости проекций, проецируется на эту плоскость в натуральную вели­чину.

Естественно, что отрезок, принадлежащий прямой общего поло­жения, не может быть равен своим проекциям (рис. 22). АВва - оче­видно неравнобочная трапеция, т.е. АВ не равнова.

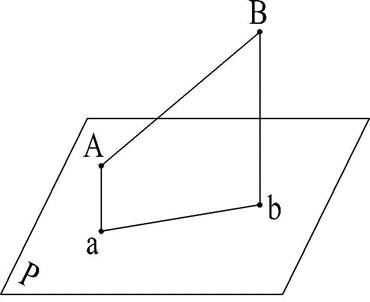Рис. 22

Отсюда возникает очень важный вопрос начертательной геометрии: "Как определить истинную длину отрезка прямой общего положе­ния?".

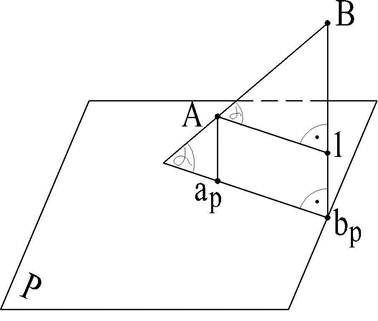Рис. 23

Пусть АВ (рис. 23) отрезок прямой общего положения, а_pв_p -его ортогональная (прямоугольная) проекция. Тогда угол Вв_pа_p = 90° (по построению). Через точку А проведем прямую A1 || а_pв_p. Cледовательно, и угол B1A = 90°. В полученном треугольнике AB1 отрезок прямой АВ является гипотенузой. Катет A1 - а_pв_p т.е. он равен проекции отрезка АВ на плоскости проекций Р. Другой катет B1 равен разности расстояний концов отрезка от плоскости проекций Р, т.е. B1 = Вв_p - Аа.

Следует обратить внимание, что угол прямой с плоскостью проекций определяется как угол, составленный прямой с ее проекцией на этой плоскости (рис. 23: угол α). Этот угол входит в тот же прямоугольный треугольник AB1, который был построен для определения натуральной величины отрезка.

Таким образом, этот способ - способ прямоугольного треуголь­ника - основан на построении прямоугольного треугольника по двум катетам, из которых один представляет длину любой из проекций, а другой является разностью расстояний концов этого отрезка от дан­ной плоскости проекций.

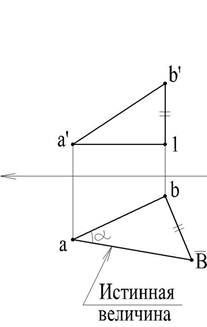На рис. 24 длина отрезка АВ и угол, составленный прямой АВ с плоскостью Н, определены из прямоугольного треугольника, пост­роенного на проекции ав со вторым катетом b B, равном в'1. АВ = a B.

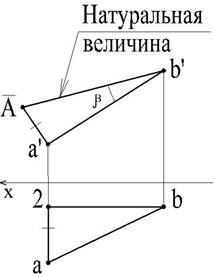Рис. 24 Рис. 25

На рис. 25 длина отрезка и угол, составленный с плоскостью V, определены из прямоугольного треугольника, построенного на фронтальной проекции а'в'. Здесь а' А = а2; а АВ = в' A. Угол наклона прямой к плоскости V равен углу β.

Тема 3. Плоскость.

3.1. Положение плоскости относительно плоскостей проекции.

Из элементарной геометрии известно, что положение плоскости и пространстве определяется:

тремя точками, не лежащими на одной прямой;

прямой и точкой, взятой вне прямой;

двумя пересекающимися прямыми;

двумя параллельными прямыми.

В соответствии с этим на чертеже (на плоскостях проекций) плос­кость может быть задана:

1. Проекциями трех точек, не лежащих на одной прямой (рис. 26)

Рис. 26

2. Проекциями прямой и точки, взятой вне прямой (рис. 27)

Рис. 27

3. Проекциями двух пересекающихся прямых (рис. 28)

Рис. 28

4. Проекциями двух параллельных прямых (рис. 29)

Рис. 29

5. Положение плоскости в пространстве определяется (может быть задано) также проекциями любой плоской фигуры (треугольника, многоугольника, круга и пр.), лежащей в данной плоскости. Пусть некоторая плоскость Р определена точками А,В,С (рис. 30)

Рис. 30

Проведя прямые через одноименные проекции этих точек, полу­чим, проекции треугольника АВС.

Если взять произвольно, например, точку Д на прямой АВ, то мы знаем, что эта точка принадлежит плоскости Р. Проводя прямую через точку Д и через другую точку, заведомо принадлежащую плоскости Р (например, через точку С), получаем еще одну прямую в плоскости Р.

Аналогично могут быть построены прямые, а, следовательно, и точки, принадлежащие плоскости, заданной любым из способов.

Все рассмотренные комбинации, определяя положение плоскости в пространстве, не дают, однако, возможности наглядно судить о том, как эта плоскость расположена относительно принятой системы плос­костей проекций. Наглядность положения плоскости может быть полу­чена только путем построения линий ее пересечения с плоскостями проекций.

3.2. Следы плоскости.

Линии пересечения некоторой плоскости с плоскостями проекций называются следами этой плоскости на плоскостях проекций.

В зависимости от того, какую из плоскостей проекций пересекает данная плоскость, ее следы называются:

- горизонтальным;

- фронтальным (вертикальным);

- профильным. Рассмотрим пространственное (рис.31) изображение некоторой плоскости и ее следов.

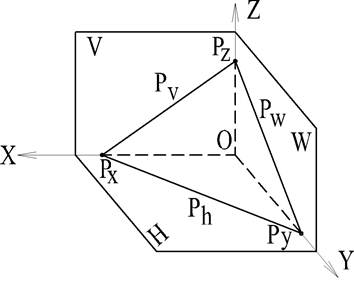Рис. 31

Принятые обозначения: Ph - горизонтальный след плоскости;

Pv - фронтальный (вертикальный) след плоскости Р;

Pw - профильный след плоскости Р;

P_x - точка схода следов на оси Х;

P_y - точка схода следов на оси Y

P_z - точка схода следов на оси Z

На рис.31 изображена плоскость, пересекающая горизонтальную плоскость проекций по прямой Pv, обозначенной Ph, фронтальную плоскость проекций - по прямой Pv и профильную - по прямой Pw.

Если плоскость пересекает ось проекций, то на этой осиполу­чается точка пересечения следов плоскости. Так как следы Pv и Ph пересекаются на оси Xв точке, обозначенной P_x; следы Phи Pw пересекаются в точке P_y; а следы Pv и Pw в точке P_z, то эти точки называют точками схода следов.

След плоскости на плоскости проекций сливается со своей проек­цией на этой плоскости. След Ph (рис. 31) сливается со своей горизонтальной проекцией; фронтальная проекция этого следа располагается на оси проекций. След Pv сливается со своей фронтальной про­екцией; горизонтальная проекция этого следа располагается на оси проекцией и т.д.

На чертеже плоскость может быть задана проекциями ее следов (рис.32). Такой чертеж нагляден и представляет удобства принекото­рых построениях.

В общем случае в системе V, H, W (рис. 31) некоторая плоскость Р пересекает все оси проекций.

На рис.31 представлено расположение плоскости Р в первом ок­танте. Плоскость Р пересекает оси X, Y, Z. Такая плоскость называется плоскостью общего положения.

Так как точки Px, Py, Pz лежат соответственно на осях X, Уи Z, то для построения чертежа плоскости в системе V, H, W достаточно иметь заданными отрезки OPx, OPy и OPz, т.е. знать координаты точек Px, Py и Pz в системе осей X, Y, Z.

Вообще каждая из этих точек имеет фактически только одну координату, т.к. две другие координаты равны нулю. Например, для построения точки Pz надо знать только ее аппликату; абцисcа и ордината этой точки равны нулю.

3.3. Положение плоскости относительно плоскости проекций.

Кроме рассмотренного нами общего положения плоскости относительно плоскостей проекций, она может занимать и частные положения, т.е. возможны следующие положения плоскости относительно плоскос­тей проекций V, H, W:

1.Плоскость не перпендикулярна ни к одной из плоскостей проекций.

2.Плоскость перпендикулярна к одной из плоскостей проекций.

3.Плоскость перпендикулярна к двум плоскостям проекций. Плоскости перпендикулярные к одной или двум плоскостям проекций называются проецирующими.

Плоскость общего положения

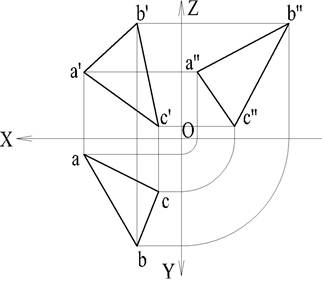Рис. 32

На рис. 32 плоскость, заданная треугольником АВС очевидно не перпендику­лярна ни к плоскости V, ни к плоскости H; Если бы она была перпендикулярна, например, к плоскости H, то проекция авс представляла бы собой отрезок прямой.

Но может быть плоскость треугольника АВС перпендикулярна W? Это легко проверить построением проекции этой плоскости на плоскость проекций W.

Следует запомнить, что следы плоскости общего положения ни­когда не перпендикулярны к осям проекций, они пересекают эти оси.

Плоскость проецирующая.

Если какая-либо плоскость перпендикулярна к одной из плоскос­тей проекций, товозможны три случая частных положений.

а) Плоскость перпендикулярна к горизонтальной плоскости проекции (рис.33)

Рис. 33

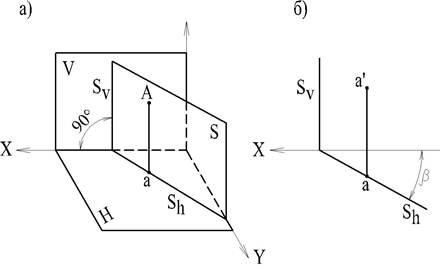
Такие плоскости называются горизонтально-проецирующими. На рис. 33а представлено пространственное изображение, а на рис.336 -чертеж в системе V, H. Из чертежа видно, что признаком горизонтально-проецирующей плоскости является то, что ее фронтальный след перпендикулярен к оси проекций X и плоскости Н.

Горизонтальный же след Sh может составлять с осью проекций любой угол. Этот угол является линейным углом двугранного угла между горизонтально-проецирующей плоскостью и плоскостью V (угол β).

Если в горизонтально-проецирующей плоскости расположена неко­торая точка (например, А), то ее горизонтальная проекция находится на горизонтальном следе плоскости Sh. Это распространяется и на любую систему точек, расположенных в горизонтально-проецирующей плоскости: прямые линии, плоские кривые линии или плоские фигуры (собирательное свойство).

б) Плоскость перпендикулярна к фронтальной плоскости проекций (рис. 34)

Рис. 34

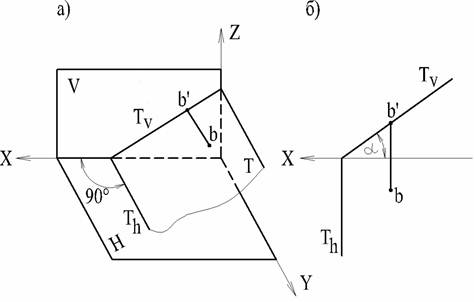
Такие плоскости называются фронтально-проецирующими. На рис. 34а представлено наглядное изображение, а на рис. 34б - чертеж в системе V, H. Из чертежа видно, что признаком фронтально-прое­цирующей плоскости является то, что ее горизонтальный след перпен­дикулярен к оси проекций X и к плоскости V.

Фронтальный же след может составлять с осью проекций Ox лю­бой угол. Этот угол является линейным углом двугранного угла между фронтально-проецирующей плоскостью и плоскостью Н (угол α).

Фронтально-проецирующая плоскость также обладает собирательным свойством. Вообще след Tv можно рассматривать (является) как фронтальную проекцию плоскости Т.

в) Плоскость перпендикулярна к профильной плоскости проекций W (рис. 35)

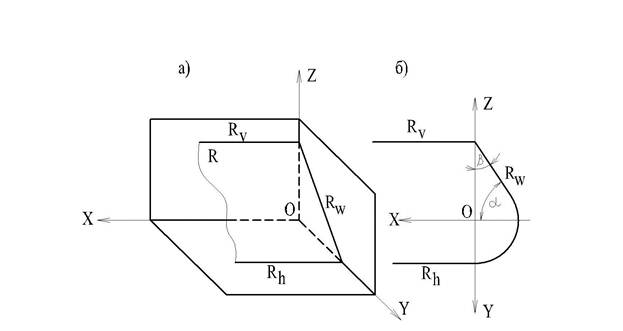Такие плоскости называются профильно-проецирующими. На рис.35а представлено наглядное изображение, а на рис.35б - чертеж в системе V, H, W с указанием осей X, Y, Zи следов плос­кости Rv, Rh, Rw.

Рис. 35

Горизонтальный Rh и фронтальный следы этой плоскос­ти параллельны оси X и, следовательно, параллельны между собой (это признак).

Профильный след Rw определяет линейные углы альфа и бета двугранник углов между профильно-проецирующей плоскостью и плоскос­тями H и V, соответственно.

3.4 Плоскость уровня

Если какая-либо плоскость перпендикулярна двум плоскостям проекций, то она называется плоскостью уровня. В этом случае также возможны три частных положения.

а) Плоскость перпендикулярна к плоскостям проекций V и W (рис.36)

Такая плоскость параллельна плоскости Н и называется гори­зонтальной или горизонтального уровня.

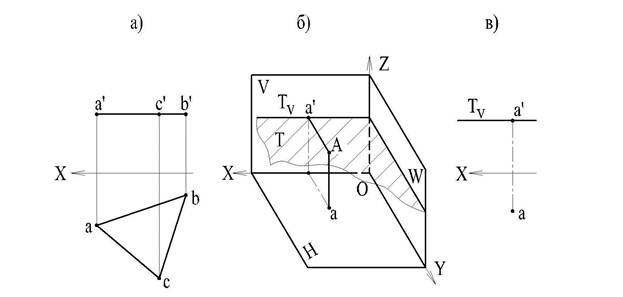
Рис. 36

В системе V, Н ее фронтальный след Tv (рис.36в) параллелен оси проекций X.

б) Плоскость перпендикулярна к плоскости проекций H и W (рис.37)

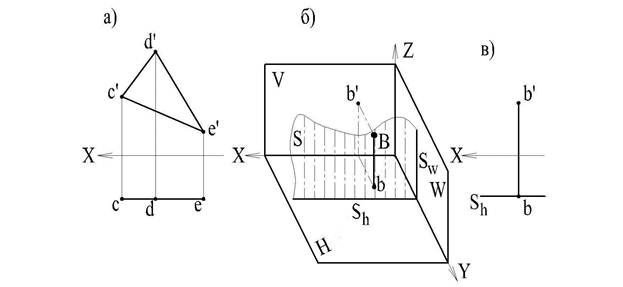Рис. 37

Такая плоскость параллельна плоскости V и называется фронтальной или фронтального уровня. В системе V, H ее горизонталь­ный след Sh (рис.38б) параллелен оси проекций X и является проекцией этой плоскости на плоскости проекций H.

в) Плоскость перпендикулярна к плоскости проекций Н и V (рис.38)

Такая плоскость называется профильной или профильного уровня.

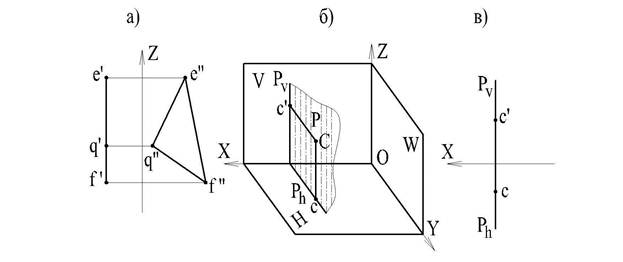
Рис. 38

На рис.38в представлен чертеж профильной плоскости в системе V, Hпри помощи ее следов. Каждый из следов можно рассматривать как проекцию плоскости Р на соответствующие плоскости проекций (см. проекции точки С).

Следует обратить внимание, что профильная плоскость сочетает в себе свойства фронтально- и горизонтально-проецирующих плоскос­тей.

3.5. ПРЯМАЯ И ТОЧКА В ПЛОСКОСТИ

Прямая относительной какой-либо плоскости может занимать сле­дующие положения:

1. Прямая лежит в плоскости.

2. Прямая параллельна плоскости.

3. Прямая пересекает плоскость.

Из элементарной геометрии известно, что:

1. Прямая принадлежит плоскости, если она проходит через две точки, принадлежащие данной плоскости.

2. Прямая принадлежит плоскости, если она проходит через точ­ку, принадлежащую данной плоскости и параллельная прямой, находя­щейся в этой плоскости или параллельной ей.

Рассмотрим пространственное (рис.39а) и плоское (рис.39б) изображение некоторой прямой MN, лежащей в плоскости общего положения Р.

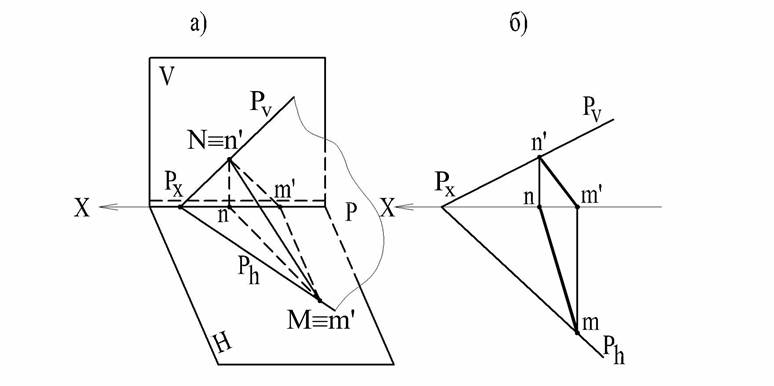
Рис. 39

По представленным фигурам легко установить правило начерта­тельной геометрии о прямой, лежащей в плоскости. Если прямая лежит в плоскости, то ее следы лежат на одноименных следах плоскости.

Можно сформулировать и второй вариант правила о прямой, ле­жащей в плоскости.

Если плоскость задана следами, то прямая принадлежит плоскости, если следы прямой находятся на одноименных с ними следах плоскости.

Это правило позволяет выполнять очень важные построения на­чертательной геометрии: построения следов плоскости, заданной проекциями точек и линий, лежащих в ней.

Например, если плоскость задана пересекающимися прямыми K и L и требуется определить положение этой плоскости в пространстве (рис.40), необходимо сначала определить следы этих прямых на плос­костях проекций и через них провести одноименные следы самой плос­кости.

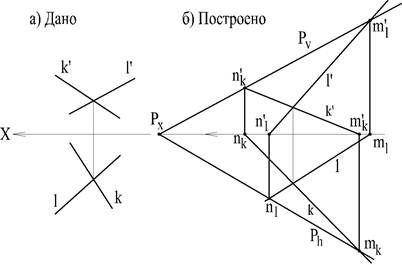Рис. 40

Это же правило позволяет провести в плоскости прямую илинаоборот, через прямую провести плоскость.

Например, необходимо провести через прямую общего положения L горизонтально-проецирующую плоскость (рис. 41).

Здесь (рис.41) направление горизонтальной прямой сливается с направлением горизонтального следа плоскости, а вертикальный след проводится из точки схода следов Px перпендикулярно оси X. Такое построение необходимо запомнить, т.к. оно часто использует­ся в задачах на пересечение прямых с геометрическими фигурами.

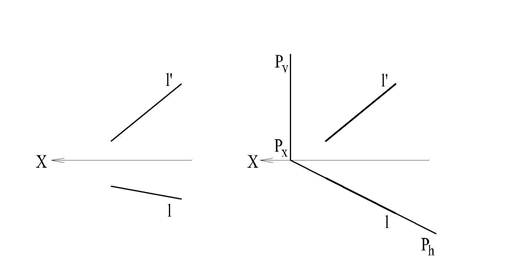
Рис. 41

Рассмотрим второе правило.

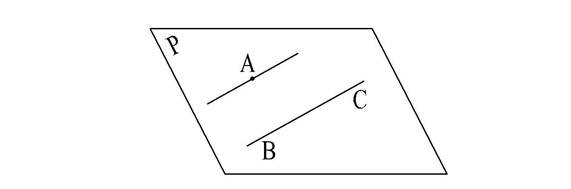Пусть плоскость Р (рис.42) определяется точкой А и прямой ВС.

Рис. 42

Согласно второму положению прямая, проведенная через точку А параллельно прямой ВС, принадлежит плоскости Р.

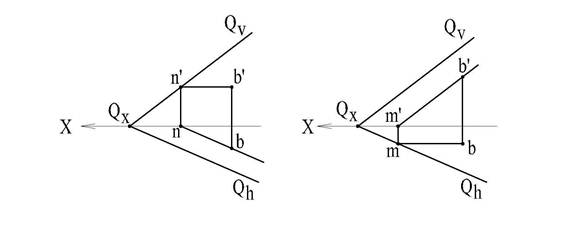Отсюда, прямая принадлежит плоскости, если она параллельна одному из следов этой плоскости и имеет с другим следом общую точку (рис. 43).

Рис. 43

3.6 Точка в плоскости

Для построения на чертеже точки необходимо сначала построить прямую, лежащую в заданной плоскости. Любая точка этой прямой будет лежать в заданной плоскости.

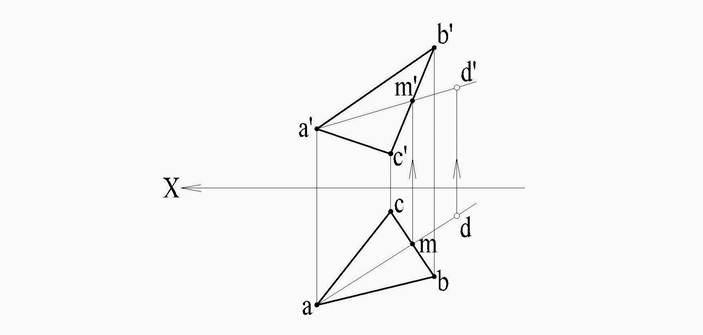Например, требуется найти фронтальную проекцию некоторой точки D, если задана ее горизонтальная проекция d и известно, что точка Dдолжна принадлежать плоскости, заданной треугольником ABC (рис.44)

Рис. 44

Порядок построения. Сначала строят горизонтальную проекцию некоторой прямой так, чтобы точка D могла оказаться на этой прямой, а сама прямая была бы расположена в данной плоскости. Для этого проводится прямая через точки а и d отмечается точка m, в которой проекция прямой ad пересекает отрезок cb. Построив фронтальную проекцию m' на b'c'получаем прямую А, расположенную в заданной плоскости. Этапрямая проходит через точки А и М, из которых первая заведомо принадлежит данной плоскости, а вторая в ней построена.

Искомая фронтальная проекция d' точки D должна быть на фронтальной проекции прямой AМ.

Таким образом, чтобы определить, лежит ли данная точка в плоскости, через нее проводится прямая, которая также должна лежать в плоскости. Если такую прямую построить нельзя, то это показывает, что точка не лежит в плоскости (рис.45).

Рис. 45

Очевидно, что точки А и С лежат в плоскости Р, а точка B находится вне этой плоскости.

Тема 4. Основные позиционные и метрические задачи

Взаимное расположение плоскостей.

В общем случае две плоскости в пространстве могут быть пара­ллельными, пересекающимися и, в частном случае, взаимноперпендикулярными.

4.1. Плоскости параллельные

Признаками параллельности двух плоскостей в общем случае слу­жит параллельность пары пересекающихся прямых одной плоскости паре пересекающихся прямых другой плоскости.

Кроме того из стереометрии известно, что две параллельные плоскости пересекаются третьей по параллельным прямым. На основа­нии этого, при изображении плоскостей следами, признаком парал­лельности плоскостей на чертеже служит параллельность их одноименных следов и одноименных проекций соответствующих линий особого положения этих плоскостей.

Чтобы судить по чертежу двух плоскостей общего положения, за­данных следами, об их параллельности пары фронтальных, горизонтальных и профильных следов должны быть взаимнопараллельны.

На рис.52 представлен чертеж параллельных плоскостей P и Q. Эти плоскости пересекаются плоскостью проекций Н по параллельным линиям Ph и Qh, а плоскостью V - по параллельным ли­ниям (следам) Pv и Qv.

Следует обратить внимание, если параллельны только две пары одноименных следов плоскостей на плоскостях проекций V и H, то для профильно-проецирующих плоскостей это не является достаточ­ным, чтобы утверждать о параллельности заданных плоскостей. Приз­наком параллельности в этом случае служит параллельность трех одноименных следов попарно.

Рис. 52

Рис. 53

Задача

Через точку Dпровести плоскость, параллельную плоскости, заданной пересекающимися прямыми АВ и АС (рис.53).

Искомая плоскость построена с помощью прямых DE и DK, соответственно параллельных АВ и АС и проходящих через заданную точку D. Одноименные проекции этих прямых параллельны.

В случае, когда некоторая плоскость P задана следами, то для построения параллельной ей плоскости, проходящей через задан­ную точку, например, B достаточно провести одну из линий особо­го положения искомой плоскости Q, например, фронталь (рис.54)

Известно, что горизонтальная проекция фронтали параллельна оси X и проходит через горизонтальную проекцию точки B(b), а вертикальная - параллельно следу Pv и проводит через фронтальную проекций b' точки В.

Горизонтальный след Qh искомой плоскости пройдет через го­ризонтальный след mфронтали, параллельно горизонтальному сле­ду Ph.Затем через точку схода Qx параллельно Pv проводится след Qv искомой плоскости Q.

4.2. Плоскости пересекаются

В результате пересечения двух плоскостей образуется линия пересечения, которая принадлежит обеим плоскостям.

Построение проекций линии пересечения двух плоскостей - это первая основная задача начертательной геометрии.

Вообще известно, что для построения линии пересечения двух плоскостей достаточно определить две любые точки, общие обеим плоскостям; либо одну общую точку и направление линии пересечения.

Линия пересечения плоскостей должна удовлетворять следующему условию:

следы линии пересечения должны лежать на одноименных следах пересекающихся плоскостей, т.е. в точках пересечения одноименных следов этих плоскостей.

Рассмотрим пространственное расположение и чертежа, прямой линии по которой пересекаются две плоскости общего положения, нап­ример, Р и Q, следы которых пересекаются в пределах черте­жа (рис.55 и 56).

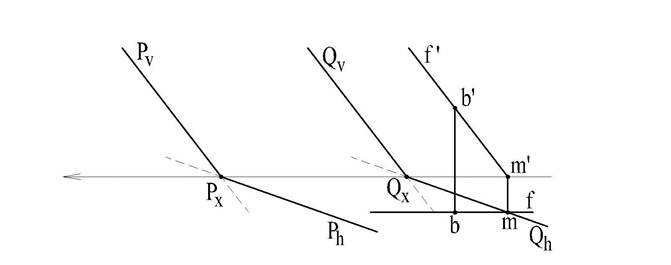
Рис. 54

Рис. 55

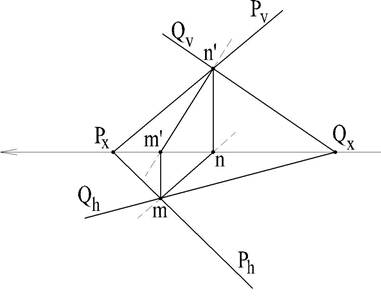Рис. 56

В точках пересечения следов лежат одноименные следы М и N линии пересечения. Соединив одноименные проекции этих точек (m и n; m' и n') получим проекции линии пересечения заданных плоскостей P и Q.

Если для построения проекций линии пересечения плоскостей общего положения необходимо определить две точки, то когда одна из пересекающихся плоскостей занимает особое положение, необходимо определить только одну общую точку, т.к. направление линии пересечения определит плоскость особого положения.

Пусть плоскость R (рис.57) параллельна плоскости Н.

Эта плоскость, очевидно, пересекает любую плоскость по гори­зонтали (h и h'). Этот вывод для данного примера обусловли­вается тем, что две параллельные плоскости R и Н пересекаются c плоскостью P по параллельным линиям. Следовательно, прямая, по которой плоскость P пересекается с плоскостью R, будет парал­лельна линии пересечения плоскости P и плоскости H, а такой линией на чертеже является след Ph. Но прямая в плоскости и параллельная Рh - есть горизонталь, а точка N (n,n')являет­ся её вертикальным следом, лежащим в точке пересечения вертикаль­ных следов пересекающихся плоскостей. Эта единственная точка N (n,n' ) позволяет построить обе проекции (h и h') линии пере­сечения плоскостей Р и R т.к. известно её направление - гори­зонталь. Фронтальная проекция линии пересечения (h' - горизонта­ли) совпадают с фронтальным следом Rvплоскости в силу его собирательного свойства, а горизонтальная проекция h - пара­ллельна Ph.

Аналогичное рассуждение применимо и к плоскости фронтальной уровня, т.е. плоскости параллельной фронтальной плоскости проекций V.

Рис. 57

4.3. Взаимное положение прямой и плоскости

Прямая по отношению к плоскости в пространстве может:

а) лежать в плоскости;

б) пересекать плоскость;

в) быть параллельной плоскости.

Прямая, параллельная плоскости

Из стереометрии известно, что прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в этой плоскости. В общем случае геометрическим местом прямых, параллельных плоскос­ти, будет плоскость, параллельная заданной.

Отсюда, признаком параллельности заданной прямой плоскости общего положения является параллельность одноименных проекций за­данной прямой и прямой, лежащей в плоскости.

Следовательно построение прямой через заданную точку парал­лельно заданной плоскости можно выполнить двумя графическими примерами:

1. В заданной плоскости взять прямую, а затем через проекции данной точки провести проекции искомой прямой так, чтобы они были бы параллельны одноименным проекциям прямой в данной плоскости.

Решим обратную задачу: например, требуется проверить парал­лельность отрезка АВ некоторой плоскости Р, заданной следами (рис.58).

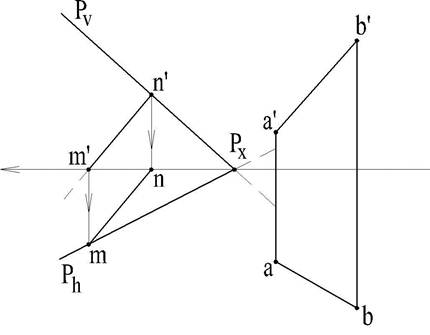Рис. 58

На фронтальном, например, следе Pv выбираем произвольно точку N (n', n) и проводим фронтальную проекцию n'm' параллельно a'b'.На оси X находим точку m', а на горизонтальном следеплоскости Ph точку m, mn - горизонтальная проекция прямой MN, принадлежащей плоскости Р. Проекция, mn очевидно не параллельна ab, следовательно, отрезок АВ (a'b',ab) не параллелен плоскости Р. 2. В заданной плоскости взять прямую, а затем через проекции и точки провести проекции искомой прямой так, чтобы они были бы параллельны одноимённым проекциям прямой в данной плоскости. Пусть плоскость задана двумя пересекающимися прямыми АВ и АС, а точка Д - её проекциями d и d' (рис.59).

Чтобы прямая Lпроходила через точку Д и была параллельна данной плоскости, необходимо, чтобы ее проекции l и l' были бы параллельны одноименным проекциям какой-либо прямой данной плос­кости.

В рассмотренном примере проекции прямой L(l,l')параллельныодноименным проекциям прямой АС заданной плоскости; сле­довательно, прямая L параллельна заданной плоскости и проходит через точку Д.

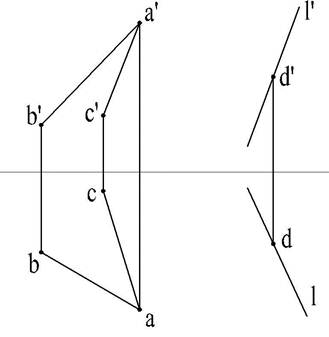
Рис. 59

4.4. Прямая, пересекающая плоскость

Прямая, не параллельная плоскости, пересекает её. Построение проекций точки пересечения прямой с плоскостью является второй основной задачей начертательной геометрии, так как она обеспечи­вает решение задач на построение проекций точек пересечения пря­мой с поверхностями многогранников, тел вращения и др.

Для определения точки пересечения прямой с плоскостью необхо­димо запомнить следующий алгоритм построения:

1. Через прямую провести вспомогательную плоскость проецирующего (в большинстве случаев) или общего положения.

2. Построить проекции линии пересечения заданной плоскости и вспомогательной.

3. Найти проекции искомой точки, которые лежат в пересечении одноименных проекций заданной прямой и линии пересечения плоскостей.

Если вспомогательная плоскость проецирующая, то одна из проек­ций искомой точки совпадает с одноименным следом этой плоскости. Видимость прямой относительно данной плоскости на плоскостях проекций V и H определяется методом конкурирующих точек.

Пусть прямая АВ пересекает плоскость общего положения P за­данную ее следами (рис.60).

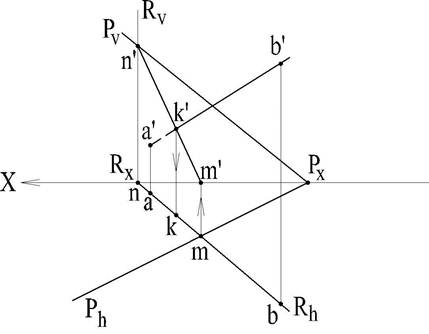Рис. 60

Решение.

1. Через отрезок АВ проведена горизонтально-проецирующая плоскость R (Rh=ab).

2. Построены проекции линии пересечения MN (mn; m'n') плоскостей P и R.

3. Определена вертикальная проекция K' искомой точки на пе­ресечении фронтальных проекций a'b' линии AB и m'n' - линии пересечения MN плоскостей R и P.

4. Горизонтальная проекция к искомой точки определена линией проекционной связи на горизонтальной проекции abотрезка АВ.

Точка К является границей видимости отрезка АВ, т.к. она ле­жит в плоскости Р, а плоскость считается не прозрачной, поэтому все что находится под плоскостью - не видимо.

Для определения видимости можно применить и в этом простейшем случае метод конкурирующих точек. В качестве таковых следует взять на плоскости V точки скрещивающихся прямых: например, следа Pv и прямой АВ, и рассматривать их положение на горизонтальной плос­кости.

Для определения видимости на горизонтальной плоскости можно взять скрещивающиеся прямые Phи АВ.

Если плоскость задана не следами, то задача построения точки пересечения прямой с плоскостью решается теми же приемами, что и с плоскостью, заданной следами (алгоритм решения задачи сохраняет­ся всегда).

4.5. Перпендикулярность прямой и плоскости

При решении задач методом начертательной геометрии нередко приходится проводить на чертежах проекции прямых, перпендикуляр­ных к различным плоскостям.

В этом случае все построения на чертежах выполняются на осно­вании теоремы о проекциях перпендикуляра к плоскости.

Теорема. Если прямая перпендикулярна к плоскости, то ее проек­ции перпендикулярны к одноименным следам плоскости, а также к со­ответствующим проекциям горизонталей, фронталей и профильных прямых данной плоскости.

Для доказательства теоремы рассмотрим пространственное изоб­ражение отрезка прямой LK перпендикулярного к некоторой плоскос­ти Р и пересекающего данную плоскость в точке К (рис.61)

Проведем в плоскости Р через точку К горизонталь NK, тогда NК перпендикулярна КL по условию. На основании теоремы о проецировании прямого угла lk перпендикулярно kn, а горизонтальная проекция горизонтали kn || Ph тогда lk перпендикулярна Ph, т.е. горизонтальная проекция перпендику­ляра к плоскости перпендикулярна к горизонтальному следу плоскос­ти и горизонтальной проекции горизонтали.

Аналогичным построением с помощью фронтали доказывается, что l'k' перпендикулярна к вертикальной проекции фронтали и вертикальному сле­ду Pv плоскости. Таким образом, если в системе V, Hгоризонтальная проекция прямой перпендикулярна горизонтальному следу и фронтальная проек­ция прямой перпендикулярна к фронтальному следу плоскости, то для плоскостей общего положения, а также горизонтально- и фронтально-проецирующих прямая перпендикулярна плоскости.

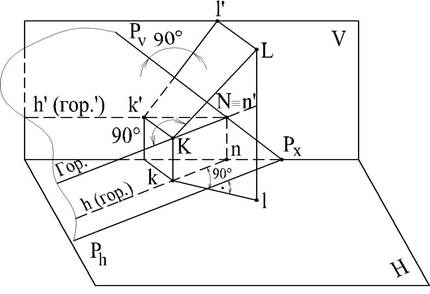Если перпендикуляр проведен к некоторой плоскости, то на этой плоскости должна быть точка их пересечения.

Рис. 61

Пусть из точки А (a,a') проведен перпендикуляр АС к плоскости Р, заданной в системе V, Н следами (рис.62).

По доказанной теореме порядок построения проекций перпендику­ляра известен:

строим a'c' перпендикулярно Pv и ac перпендикулярно Ph