Основные виды кривых второго порядка на плоскости

Название кривой	Вид уравнения	Основные сведения о кривой	Вид кривой
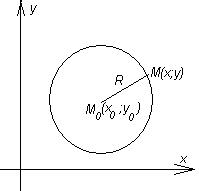
Окружность		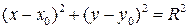R – радиус Центр в точке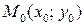
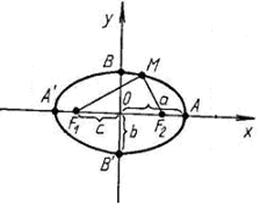
Эллипс		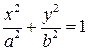a – большая полуось, b – малая полуось Вершины эллипса А (а; 0), А ’(–a; 0), В (0; b), В ’(0; – b) с – фокусное расстояние, 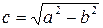Фокусы F 1(c; 0), F 2(– c; 0) e – эксцентриситет,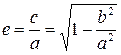
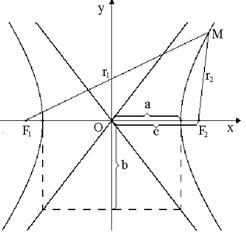
Гипербола		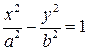a – действительная полуось, b – мнимая полуось Вершины гиперболы А (а; 0), А’ (–a; 0), с – фокусное расстояние, 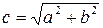Фокусы F 1(c; 0), F 2(– c; 0) e – эксцентриситет, 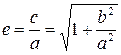Асимптоты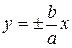
Парабола		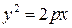р – параметр параболы ОХ – ось симметрии Фокус F (р /2; 0) Директриса y = –p / 2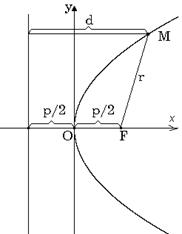
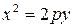
	р – параметр параболы ОУ – ось симметрии Фокус F (0; р /2), Директриса y = –p / 2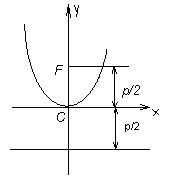

Уравнение 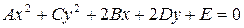всегда определяет:

– окружность, при А = С,

– эллипс, при АС >0,

– гиперболу, при АС <0,

– параболу, при АС = 0.

При этом возможны случаи вырождения:

– для эллипса (окружности) – в точку или мнимый эллипс (окружность);

– для гиперболы – в пару пересекающихся прямых;

– для параболы – в пару параллельных прямых.