Вектора
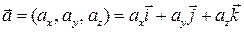
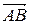 = (x 2 – x 1; y 2– y 1; z 2– z 1)
= (x 2 – x 1; y 2– y 1; z 2– z 1)
Длина вектора
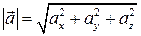 или
или 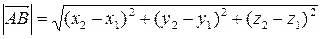
Направляющие косинусы вектора
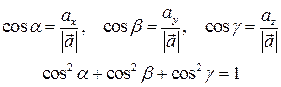
Единичный вектор
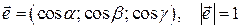
Орт вектора 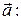
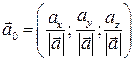
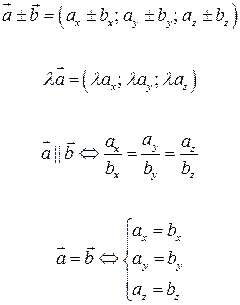
| Скалярное произведение | Векторное произведение | Смешанное произведение |
Число
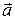 × × 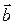 = ï = ï 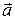 ïï ïï 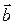 ï cosj ï cosj
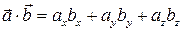
| Вектор
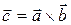
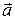 ´ ´ 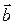 = = 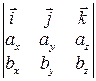
| Число
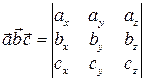
|
Свойства:
1) 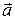 × × 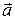 = ï = ï 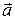 ï2;
2) ï2;
2) 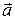 × × 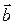 = 0, если = 0, если 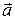 ^ ^ 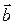 ;
3) ;
3) 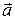 × × 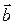 = = 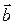 × × 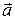 ; ;
| Свойства:
1) 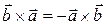 ;
2) ;
2) 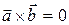 , если , если 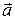 ïï ïï 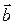
| Свойства:
1) 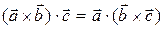 2)
2) 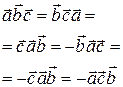 3)
3) 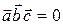 , если вектора компланарны , если вектора компланарны
|
Приложения:
Угол между векторами
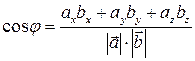 Проекция вектора на вектор
Проекция вектора на вектор
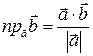
| Приложения:
Площадь параллелограмма
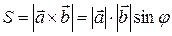
| Приложения:
Объем параллелепипеда и пирамиды
V = 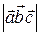 Vпир =
Vпир = 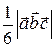
|
Прямая на плоскости
Основные типы уравнений прямых на плоскости
| Название | Уравнение | Что дано | Иллюстрация |
| Общее | Ах + Ву + С = 0 | Коэффициенты А и В – координаты нормального вектора 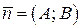
| |
| С угловым коэффициентом | 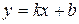
| 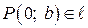 угловой коэффициент k или угол наклона α
угловой коэффициент k или угол наклона α
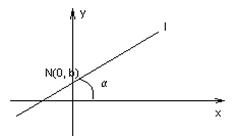
| 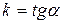 – угловой коэффициент,
b – ордината точки пересечения прямой с осью ОУ – угловой коэффициент,
b – ордината точки пересечения прямой с осью ОУ
|
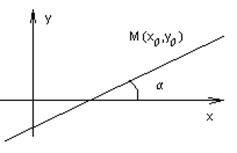
| В данном направлении | 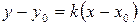
| 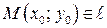 ,
угловой коэффициент k или угол наклона α ,
угловой коэффициент k или угол наклона α
| 
|
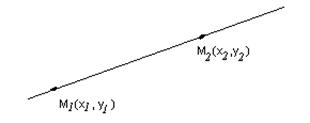
| Через две точки | 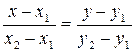
| 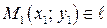
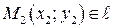
| 
|
| В отрезках | 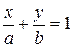
| Прямая отсекает на координатных осях отрезки a и b | 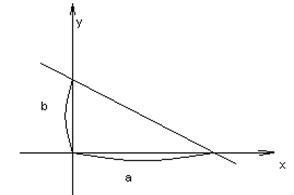
|
| Перпендикулярно вектору | 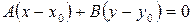
| 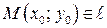
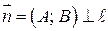
| 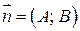 – нормальный вектор – нормальный вектор
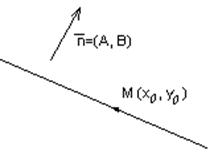
|
| Каноническое | 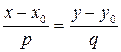
| 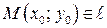
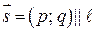
| 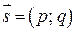 – направляющий вектор – направляющий вектор
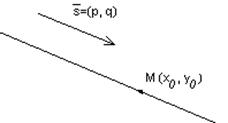
|
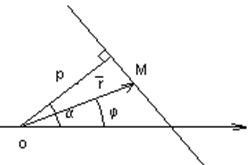
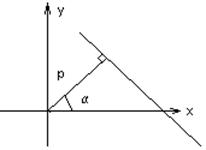
| Полярное | 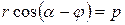
| р – расстояние от начала координат до прямой, 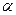 – угол отклонения перпендикуляра р от координатной оси – угол отклонения перпендикуляра р от координатной оси
| 
|
| Нормальное | 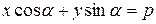
| р – расстояние от начала координат до прямой, 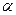 – угол отклонения перпендикуляра р от оси ОХ – угол отклонения перпендикуляра р от оси ОХ
| Нормирующий множитель
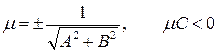 (общее→нормальное)
(общее→нормальное)
|
 2015-04-12
2015-04-12 248
248







