Момент инерции материальной точки

Представим себе материальную точку, движущуюся по окружности радиуса 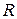. При вращательном движении линейная 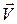и угловая 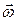скорости связаны соотношением:

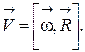
Поэтому выражение для момента импульса в этом случае примет следующий вид:

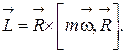(2.6.1)

Двойное векторное произведение (2.6.1) может быть представлено как

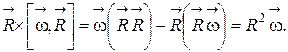
Окончательно получаем выражение для момента импульса материальной точки, вращающейся относительно некоторой оси:

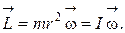(2.6.2)

Моментом инерции 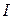материальной точки называется физическая величина, равная произведению массы точки 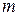на квадрат расстояния 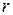от этой точки до некоторой оси:

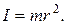(2.6.3)

Очевидно, что момент инерции точки будет разным относительно разных осей.