Момент количества движения материальной точки

Пусть имеется материальная точка массой 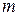, на которую действует сила 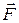. Уравнение движения точки имеет вид:

.

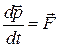Умножим обе части этого уравнения векторно на радиус-вектор 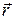, в результате получим:

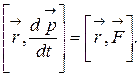(2.5.1)

В правой части (3.5.1) мы получили выражение для момента силы относительно выбранной оси. Левую часть (3.5.1) преобразуем, используя правила векторного исчисления. Вычислим производную по времени от векторного произведения :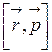

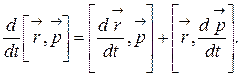
Учтем, что 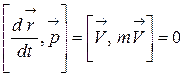, и получим:

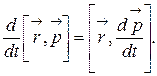
Моментом количества движения или моментом импульса отдельной частицы (материальной точки) относительно произвольно выбранной фиксированной точки (фиксированной в инерциальной системе отсчета) определяется соотношением (рис. 2.5):

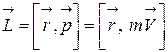. (2.5.2)

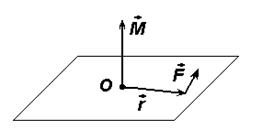
Рис. 2.5. К определению момента импульса материальной точки

Тогда выражение (2.5.2) примет вид:

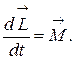(3.5.3)

Итак, скорость изменения момента импульса равна моменту сил.
Это важное соотношение называется уравнением моментов.