Теоретические сведения. Многослойный персептрон является сетью с прямым распространением сигнала (без обратных связей), обучаемой с учителем

Многослойный персептрон является сетью с прямым распространением сигнала (без обратных связей), обучаемой с учителем. Такая сеть способна аппроксимировать любую непрерывную функцию или границу между классами со сколь угодно высокой точностью. Для этого достаточно одного скрытого слоя нейронов с сигмоидной функцией активации (2) – (4), т.е. многослойный персептрон обычно состоит из 3 слоев: первого распределительного, второго скрытого и третьего выходного (рис. 2.1).

Рис. 2.1. Многослойный персептрон

Такая сеть имеет n входов и n нейронов распределительного слоя, h нейронов скрытого слоя и m выходных нейронов. Используются две матрицы весов: скрытого слоя v размером n ´ h и выходного слоя w размером h ´ m. Кроме этого, с каждым слоем нейронов связан массив порогов: Q – для скрытого слоя, T – для выходного. Эти данные представляют собой знания сети, настраиваемые в процессе обучения и определяющие ее поведение. Персептрон функционирует по следующим формулам:

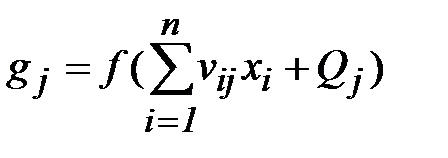, (2.1)

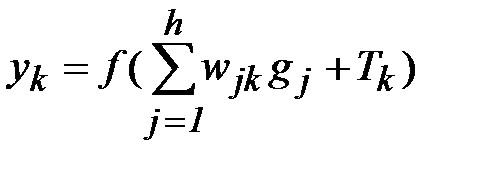. (2.2)

В качестве функции активации используется одна из функций (2) – (4). Вид функции определяет диапазон чисел, в котором работает сеть. В дальнейшем будет использоваться сигмоидная функция (2), имеющая область значений от 0 до 1.

Обучение с учителем ставит перед сетью задачу обобщить p примеров, заданных парами векторов (x^r, y^r), 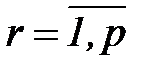. Вектор 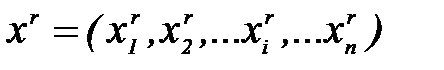в случае задачи классификации задает входной образ (вектор признаков), а вектор 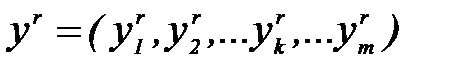, задающий эталонный выход, должен кодировать номер класса. При этом есть множество вариантов кодирования. Оптимальным представляется кодирование, когда номер класса определяется позицией единичной компоненты в векторе y^r, а все остальные компоненты равны 0. Каждый выходной нейрон соответствует одному классу. Такой способ позволяет при классификации определять вероятность каждого класса по величине на выходе соответствующего нейрона (чем ближе к единице, тем вероятность больше).

Обучение персептрона проводится с помощью алгоритма обратного распространения ошибки, который минимизирует среднеквадратичную ошибку нейронной сети. Для этого с целью настройки синаптических связей используется метод градиентного спуска в пространстве весовых коэффициентов и порогов нейронной сети. Рассмотрим алгоритм обратного распространения ошибки.

1. Происходит начальная инициализация знаний сети. Простейший вариант такой инициализации – присвоить всем весам и порогам случайные значения из диапазона [-1,1].

2. Для каждой пары векторов (x^r, y^r) выполняется следующее:

2.1. Для входного вектора рассчитываются выходы нейронов скрытого слоя и выходы сети по формулам (2.1), (2.2).

2.2. Происходит коррекция знаний сети, при этом главное значение имеет отклонение реально полученного выхода сети y от идеального вектора y^r. Согласно методу градиентного спуска, изменение весовых коэффициентов и порогов нейронной сети происходит по следующим формулам:

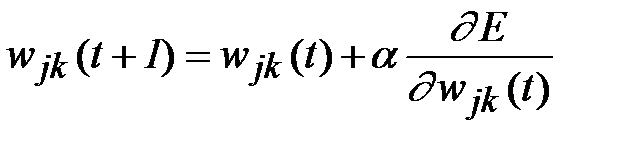, (2.3)

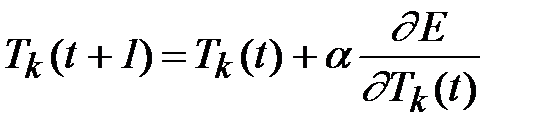, (2.4)

где E - среднеквадратичная ошибка нейронной сети для одного образа, а a – параметр, определяющий скорость обучения. Формулы записаны в терминах выходного слоя, аналогично выглядят формулы для скрытого слоя. Среднеквадратичная ошибка сети вычисляется как

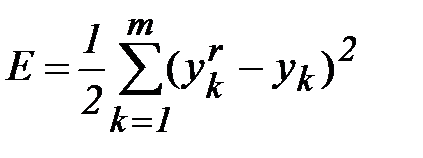. (2.5)

Ошибка k -го нейрона выходного слоя определяется как

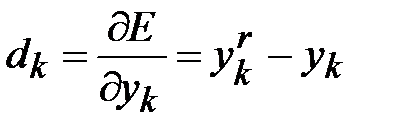. (2.6)

Выразим производные из формул (2.3), (2.4) через легко вычисляемые величины. Определим взвешенную сумму, аргумент функции активации как

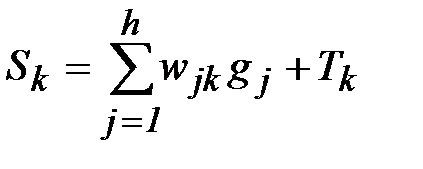. (2.7)

Из соотношения (3.3) 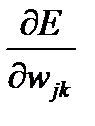можно представить как:

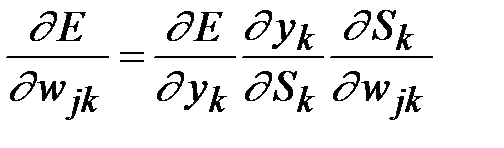, (2.8)

где 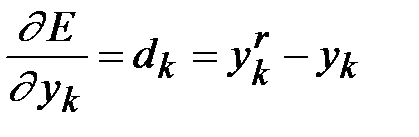– ошибка k -го нейрона; 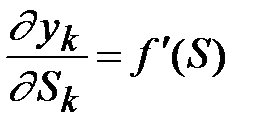– производная функции активации; 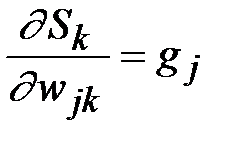– значение j -го нейрона предыдущего слоя. Получаем

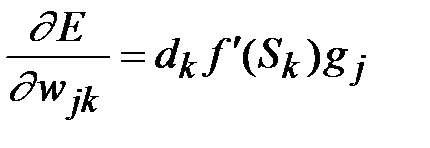. (2.9)

Аналогично (2.8), с учетом того, что 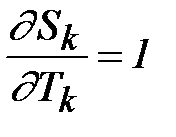, получаем

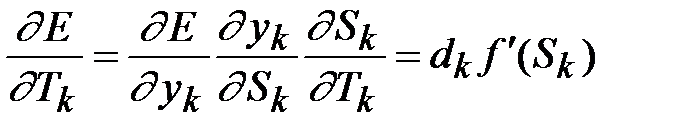. (2.10)

Веса и пороги скрытого слоя также корректируются по формулам, аналогичным (2.3), (2.4), с учетом (2.9) и (2.10). При этом главной трудностью является определение ошибки нейрона скрытого слоя. Эту ошибку явно определить по формуле, аналогичной (2.6), невозможно, однако существует возможность рассчитать ее через ошибки нейронов выходного слоя (отсюда произошло название алгоритма обратного распространения ошибки):

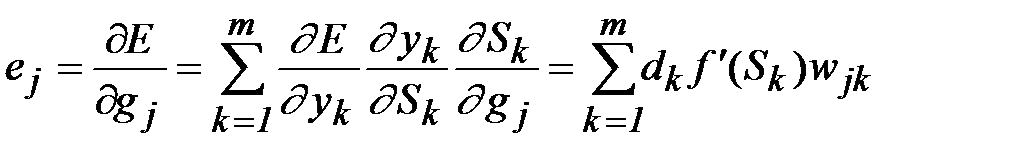. (2.11)

Производные от функций активации тоже легко рассчитываются, например, для сигмоидной функции получаем

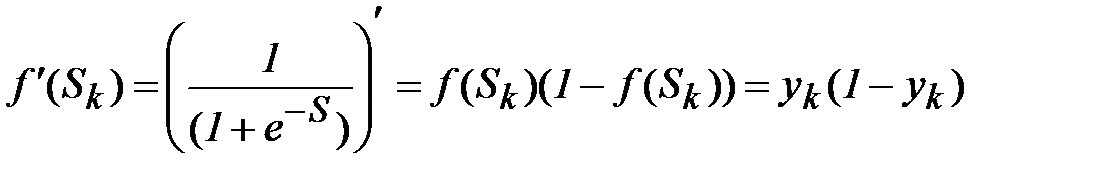. (2.12)

Аналогично

;

.

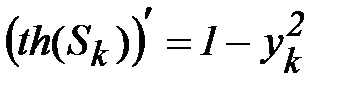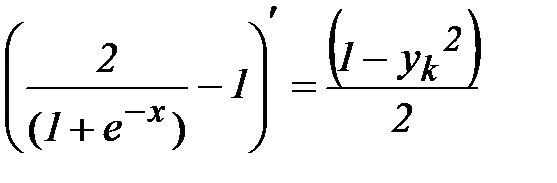Таким образом, можно записать окончательные выражения (2.3), (2.4) для двух слоев, использующих сигмоидную функцию:

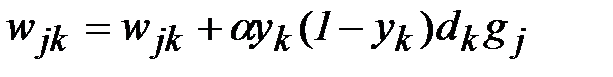, (2.13)

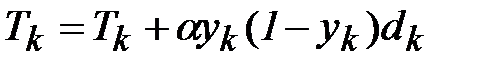, (2.14)

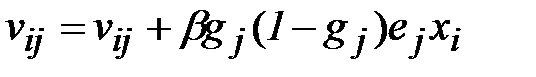, (2.15)

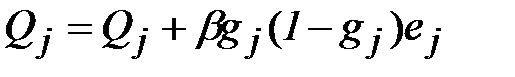. (2.16)

В эти формулы вводится дополнительный параметр b – скорость обучения скрытого слоя, который может отличаться от аналогичного параметра для выходного слоя. Рекомендуется изменять скорости обучения обратно пропорционально количеству шагов алгоритма обучения, однако это не всегда оправдывает себя на практике.

3. После того как коррекция знаний произведена для каждой пары векторов, можно оценить степень успешности обучения сети для определения момента завершения алгоритма. Для этого можно использовать в качестве критерия максимальную по модулю ошибку на выходе d_k, полученную на шаге 2. Условием прекращения обучения в этом случае будет

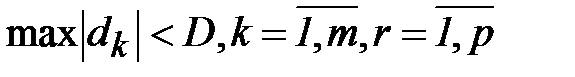, (2.17)

где D – достаточно маленькая константа – величина максимальной ошибки, которую требуется достичь в процессе обучения. Если условие (2.17) не выполняется, то шаг 2 повторяется.

Способность персептрона-классификатора разделять образы в пространстве признаков прежде всего зависит от его скрытого слоя. Именно на этот слой возлагается задача сделать множество классов линейно разделимым для успешной работы выходного слоя. Очевидно, что чем больше нейронов в скрытом слое, тем большее количество примеров этот слой может разделять. Кроме этого, увеличение числа признаков входных образов также способствует успешному их разделению в пространстве признаков. Однако увеличение этих параметров приводит к росту ошибок сети и времени обучения. Увеличение размерности входов n приводит к росту ошибки аппроксимации сети, возникающей из-за обобщения данных. Увеличение числа нейронов h скрытого слоя приводит к росту ошибки, связанной со сложностью модели. Персептрону легче провести функцию через эталонные точки, однако при этом обобщающая способность сети ухудшается. Он хуже предсказывает поведение аппроксимируемой функции на образах, не входящих в обучающую выборку. Такое состояние сети называется переобучением.

Оптимальное соотношение между этими параметрами оценивают как

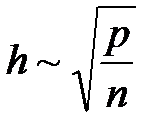. (2.18)

Эксперименты показывают, что обучение максимально успешно проходит на множестве классов, хорошо (желательно линейно) разделенных в пространстве признаков. Это достигается удачным подбором информативных признаков. Если классы в пространстве признаков хорошо кластеризуются, т.е. образы каждого класса составляют компактную группу, достаточно удаленную от других групп, то есть возможность уменьшить размер обучающей выборки p (используются только центры кластеров) и затем уменьшить число нейронов h. Это приводит к ускорению обучения и улучшает работу классификатора.

Другой проблемой является то, что алгоритм градиентного спуска не гарантирует нахождение глобального минимума среднеквадратичной ошибки сети (2.5), а гарантируется определение только локального минимума. Проблемы, возникающие в процессе градиентного спуска, можно проанализировать на примере функции ошибки, схематически изображенной на рис. 2.2.

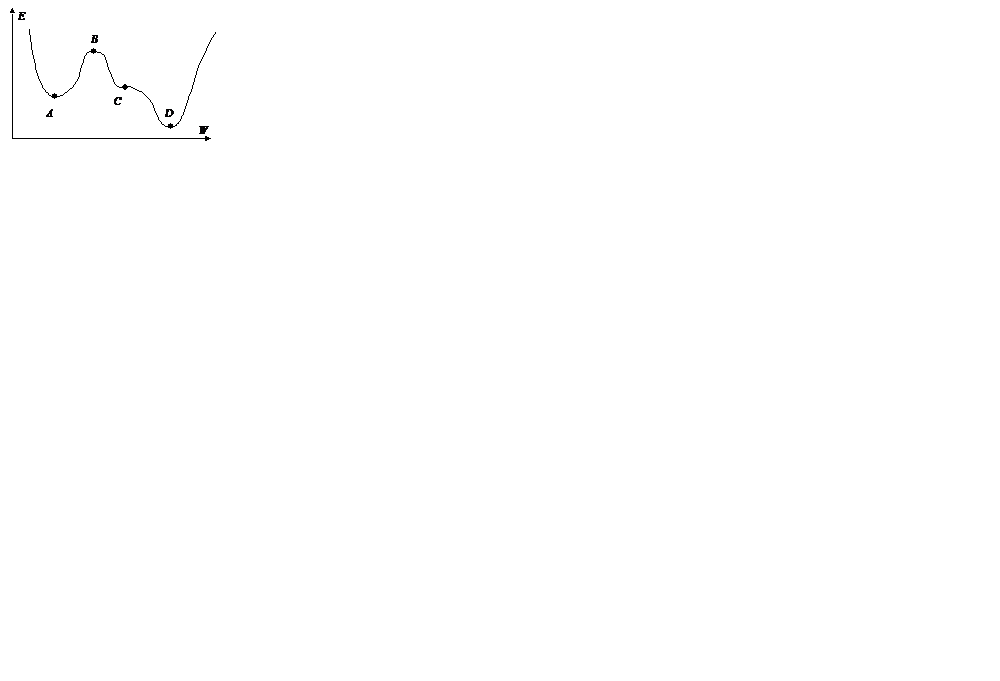
Рис. 2.2. Схематическая функция ошибки сети

На рис. 2.2 показаны четыре критические точки, производная функции ошибки в которых близка к нулю. Точка A соответствует локальному минимуму. Признаком достижения локального минимума в процессе обучения является полное прекращение уменьшения ошибки (2.17). В этом случае может помочь повторное обучение с другим начальным распределением знаний (тут может помочь случайная инициализация). Точка B – локальный максимум. В случае попадания в окрестность такой точки скорость резко падает, затем снова быстро растет. Не существует способа предсказать, в какую сторону лучше двигаться из точки с производной, близкой к нулю. Точка C – точка перегиба, характеризуется длительным уменьшением скорости. Точка D – глобальный минимум – цель алгоритма.

Существуют многочисленные способы оптимизации метода градиентного спуска, призванные улучшить поведение алгоритма в подобных критических точках. Эффективной модификацией является введение момента, накапливающего влияние градиента на веса со временем. Тогда величина Dw (2.3) в момент времени t будет вычисляться как

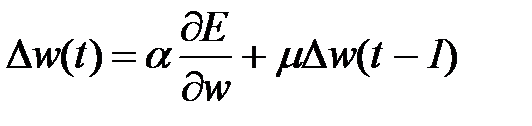, (2.19)

где m – параметр, определяющий величину влияния момента. С использованием (2.19) скорость изменения весов возрастает на участках с постоянным знаком производной. В окрестностях минимума скорость резко падает за счет колебания знака.

Достоинства алгоритма – большая скорость в точках перегиба, возможность по инерции преодолевать небольшие локальные минимумы. Недостатки – еще один параметр, величину которого следует подбирать и настраивать.

Этот и другие алгоритмы оптимизации обучения персептрона позволяют улучшить работу сети в условиях плохой сходимости. Однако они усложняют процесс обучения, не гарантируя в то же время полного успеха во всех случаях. Успех обучения классификатора зависит от самого алгоритма обучения и качества обучающей выборки.