Геометрические тела с вырезом

Пример 1. Вырез на конусе (рис.142).

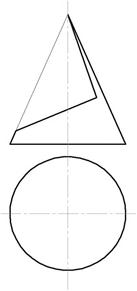
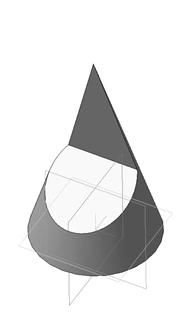Рис.142

Вырез произведен двумя плоскостями. Одна проходит через вершину конуса и рассечет его поверхность по образующим. Вторая плоскость - фронтально-проецирующая, линия пересечения – часть эллипса, ограниченная прямой принадлежащей линии пересечения плоскостей.

1. Отметим фронтальные проекции характерных точек для построения выреза - А'', В'', С'', M",N" (рис. 143).

2. Точки D и Е выбраны произвольно для построения эллипса, т.к. линия среза от А до СN представляет собой часть эллипса.

3. Найдем горизонтальные проекции точек А, В, С, D, Е, N. Точки лежат на поверхности конуса, а значит, они лежат на линиях, принадлежащих поверхности конуса. Горизонтальные проекции точек М и В, D и E найдены на окружностях, принадлежащих поверхности конуса. Точки С и N - на образующих S₁ и S₂.

4. Соединяем полученные горизонтальные проекции. S'С' и S'N' – прямые, C', B', D', A', E', M', N' – кривая линия - часть эллипса (рис. 142).

Рис.143 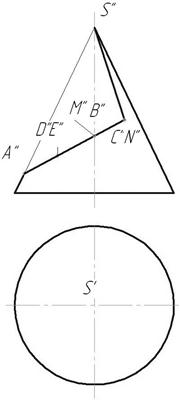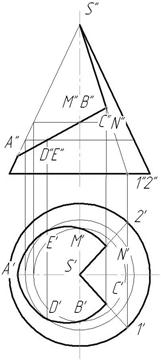Рис.144

Строим профильную проекцию конуса и профильные проекции точек. Соединяем их (рис.145).

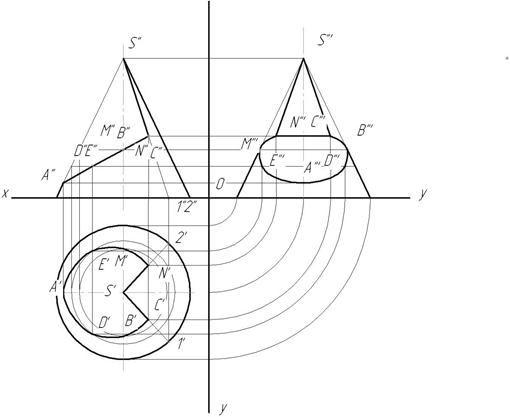
Рис.145

Пример 2. Вырез на цилиндре (рис.146).

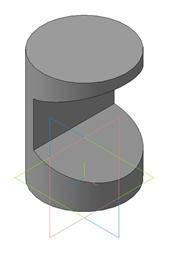
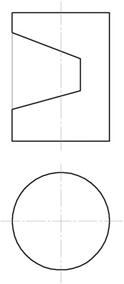
Рис. 146

Вырез произведен тремя плоскостями. Наклонные фронтально-проецирующие плоскости рассекут цилиндр по части эллипса, ограниченного прямой. Плоскость, параллельная оси вращения, пересекает поверхность цилиндра по образующим.

1. Отметим на фронтальной проекции выреза фронтальные проекции A",F",G",K",L",P". Характерные точки D",E" ,M",N" - на оси симметрии цилиндра, B",C",T",V " - отмечены произвольно на линии, принадлежащей поверхности цилиндра. Все точки принадлежат боковой поверхности цилиндра, которая проецируется в окружность на горизонтальной плоскости проекций. Поэтому все горизонтальные проекции точек принадлежат этой окружности (рис.147).

Рис.147

Найдем профильные проекции всех точек. Затем полученные точки соединяем. Линия GECABDF - часть эллипса, FK и GL отрезки прямых, GF и KL-отрезки прямых, LNVPTMK - часть эллипса (рис. 148).

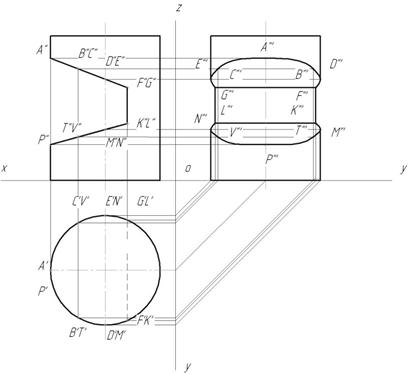Рис.148

Пример 3. Вырез на призме (рис.149).

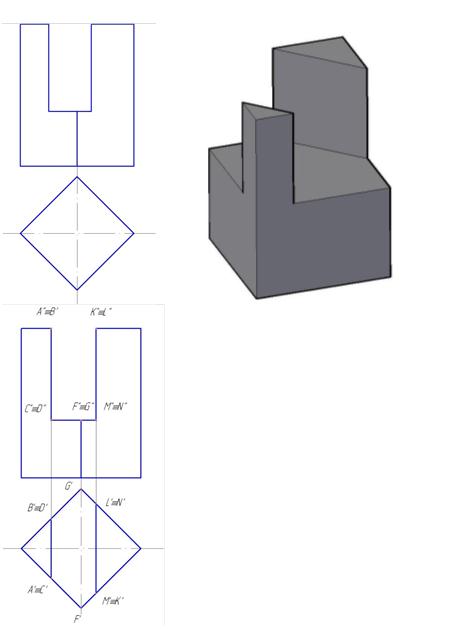Рис.149 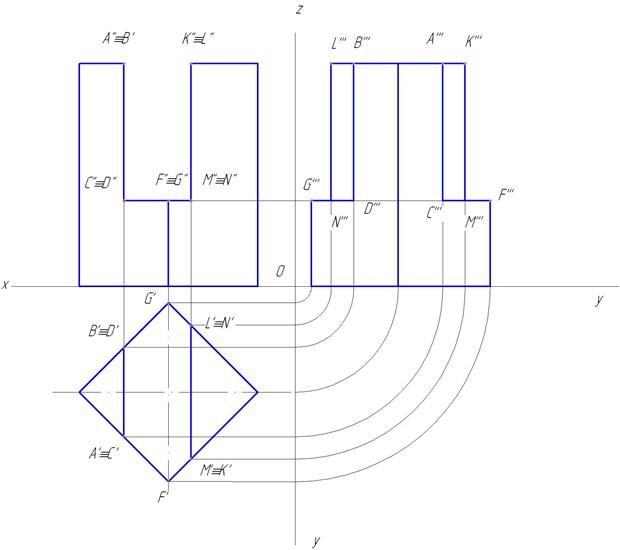Hbc

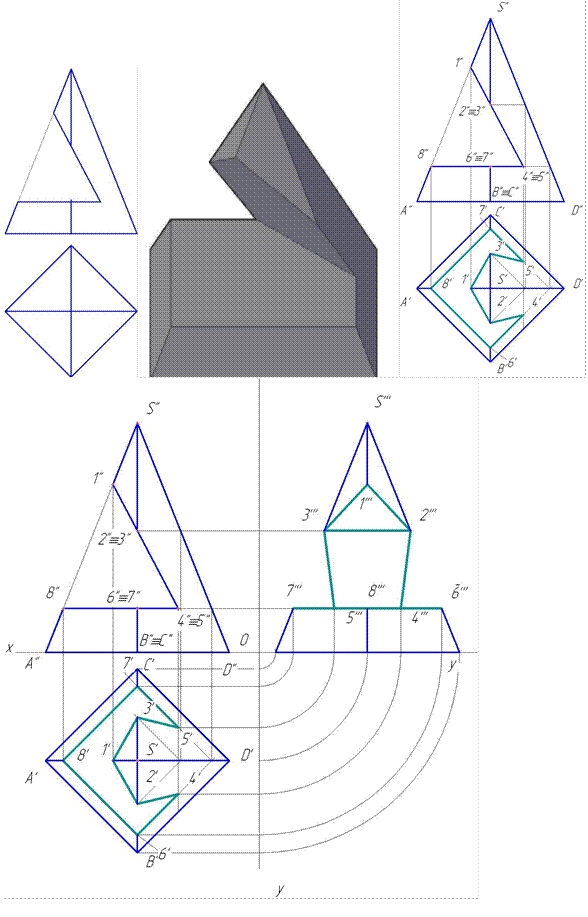
Рис. 150

Пример 4. Вырез на пирамиде (рис.150).

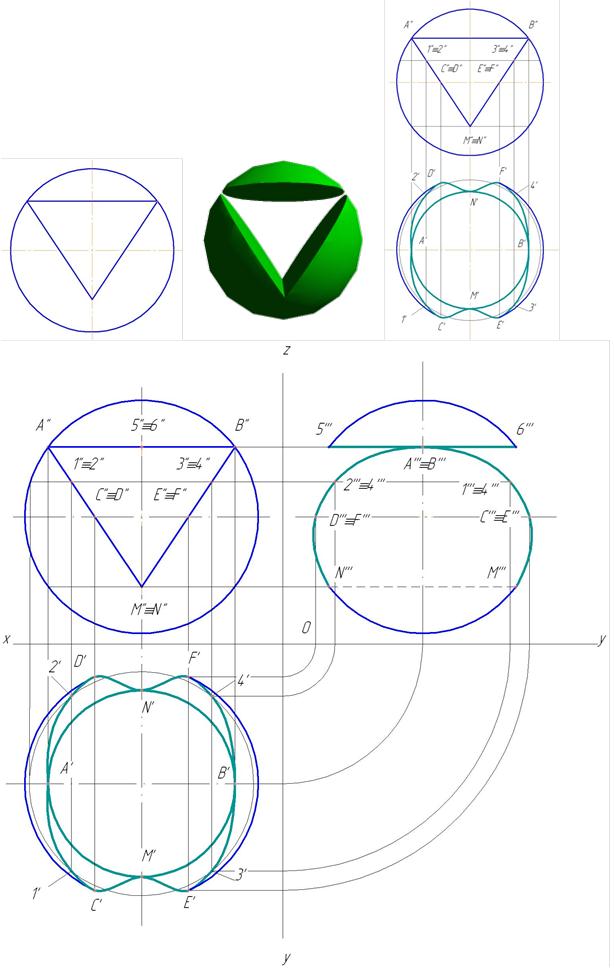
Пример 5. Вырез на сфере (рис. 151

p>