2015-06-28
9102
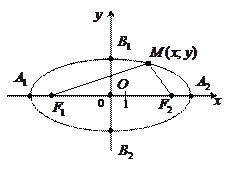
Определение: эллипсом называется геометрическое место точек плоскости, сумма расстояний каждой из которых до двух данных точек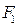 
и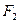 
(называемых фокусами) есть величина постоянная, равная 
.
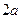Чертеж эллипса: выберем прямоугольную систему координат так, чтобы ось Ox проходила через фокусы 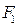и (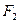
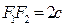), а начало координат находилось в середине 
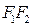. Фокусы будут иметь координаты 
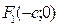и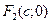 
. Пусть 
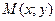– произвольная точка эллипса. По определению эллипса 
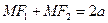или по формуле расстояний: 
, 
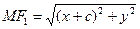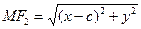, т.е. 
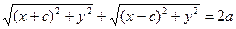– это и есть уравнение эллипса.
Канонический (простейший) вид уравнения эллипса:
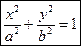– каноническое уравнение эллипса.
Заметим, что
1) 
;
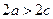2) 
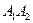– большая ось эллипса, 
;
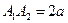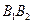– малая ось эллипса, 
;
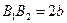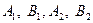– вершины эллипса;
3) Эксцентриситет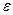 
эллипса – отношение расстояния между фокусами к длине его большой оси, т.е. 
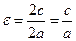. Он характеризует степень сжатия эллипса: чем больше 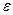тем больше вытянут эллипс.
4) Величины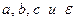 
– параметры эллипса.
