Способ замены плоскостей проекций. Сущность способа замены плоскостей проекций состоит в том, что заданную систему плоскостей проекций заменяют новой системой так

Сущность способа замены плоскостей проекций состоит в том, что заданную систему плоскостей проекций заменяют новой системой так, что геометрические фигуры оказываются в частном положении относительно новой системы плоскостей проекций.

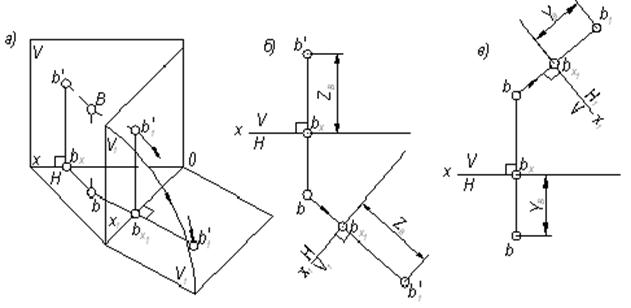
Рис. 5.1

Проследим, как изменятся проекции точки B, если плоскость V заменить на новую плоскость проекций V₁ (рис. 5.1, а). Плоскость V₁ проводим перпендикулярно плоскости Н, положение которой остается без изменения. Плоскости Н и V₁ пересекутся по прямой 0х₁, определяющей новую ось проекций. В новой системе плоскостей проекций вместо проекций b и b' получим новые проекции b и b₁′. Легко убедиться, что расстояние от новой проекции точки b₁′ до новой оси 0х₁ (координата Z) равно расстоянию от заменяемой проекции b' до заменяемой оси 0х. Чтобы перейти от пространственного чертежа к эпюру, нужно совместить плоскость V₁ с плоскостью Н. На эпюре (рис. 5.1, 6) для построения новой проекции b₁′ используем неизменность координаты Z точки B. Для этого достаточно из горизонтальной проекции b провести перпендикуляр к новой оси 0х₁ и от точки b_X1 отложить координату Z, определяемую расстоянием b'b_x (Z_B) в прежней системе.

Замена горизонтальной плоскости Н новой плоскостью Н₁ (рис. 5.1, в) производится аналогично, с той лишь разницей, что теперь не изменяется фронтальная проекция точки b', для построения новой горизонтальной проекции b₁ необходимо из сохраняемой фронтальной проекции b' провести линию связи к новой оси 0х₁ и отложить от новой оси расстояние, равное расстоянию от заменяемой проекции b до заменяемой оси 0х.

Замена плоскостей проекций может осуществляться только последовательно, нельзя менять обе плоскости сразу.

Рассмотрим на примерах, как производится замена плоскостей проекций и строятся новые проекции фигур.

Задача 1. Определить длину отрезка прямой АВ общего положения.

Заменяем плоскость V плоскостью V₁, параллельной отрезку АВ (рис. 5.2, а). Проводим новую ось Х₁ параллельно ab и на перпендикулярах, проведенных к ней из точек а и b, откладываем а_X1а₁′ = а_xа' и b_X1b₁′ = b_xb'. Получаем новую проекцию a₁′b₁′ = AB и одновременно угол α наклона прямой к плоскости Н.

Если плоскость Н заменим плоскостью H₁ параллельной отрезку АВ (рис. 5.2, б), то получим а₁b₁ = АВ и угол β наклона прямой к плоскости V.

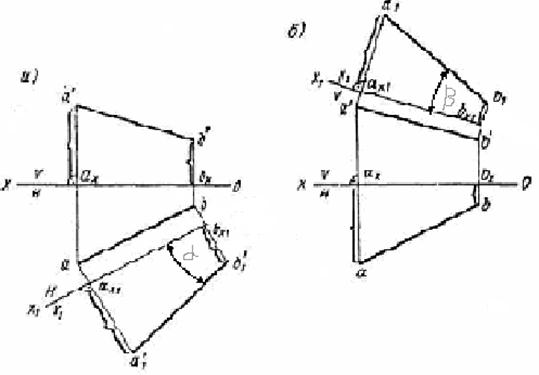
Рис. 5.2

Задача 2. Определить натуральную величину и форму треугольника ABC.

Задача решается последовательной заменой двух плоскостей проекций.

Сначала плоскость V заменяем плоскостью V₁, перпендикулярной к плоскости треугольника (рис. 5.3). Для этого в плоскости треугольника проводим горизонталь AD (ad, a'd') и новую ось Х₁ располагаем перпендикулярно к ad. На новой плоскости проекций треугольник спроецируется в прямую b₁′а₁′с₁. На втором этапе плоскость Н заменяем плоскостью Н₁, параллельной плоскости треугольника, располагая ось Х₂ параллельно прямой b₁′а₁′с₁′. Построенная проекция a₁b₁с₁ определяет натуральную величину и форму треугольника ABC.

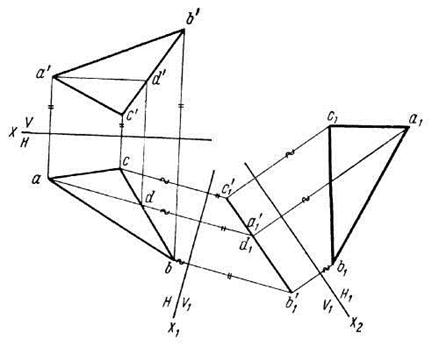Рис. 5.3

Задача 3. Определить расстояние от точки А (а, а') до плоскости Р, заданной следами P_H и P_V (рис. 5.4).

Задача решается путем замены одной из плоскостей проекций новой, относительно которой плоскость Р будет проецирующей.

Заменим, например, плоскость V плоскостью V₁, перпендикулярной к плоскости Р. Новую ось X₁ проводим перпендикулярно к следу Р_Н. Выбираем на следе P_V произвольную точку N (п, п') и находим ее новую проекцию п₁′,откладывая n_X1n₁′ = n_xn' = y_N.. Через точки P_X1 и п₁′ проводим новый след P_V1. Построив новую проекцию a₁′ и опустив из нее перпендикуляр на P_V1, определяем расстояние от точки А до плоскости Р, которое равно отрезку a₁′k₁′. После этого определяем на первоначальном чертеже положение проекции основания перпендикуляра (k, k′).

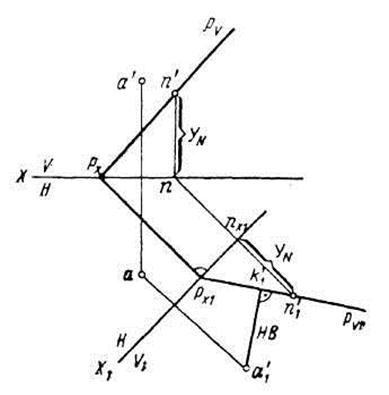
Рис. 5.4

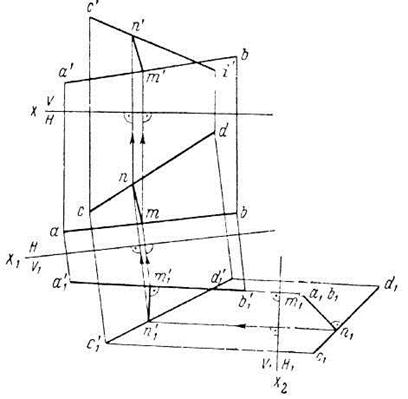Задача 4. Определить кратчайшее расстояние между двумя скрещивающимися прямыми АВ (ab, a^′b′)и CD (cd, c'd')(рис. 5.5).

Рис. 5.5

Отрезок перпендикуляра к обеим прямым, измеряющий кратчайшее расстояние между ними, проецируется в натуральную величину на плоскость проекций, перпендикулярную к одной из скрещивающихся прямых.

Для решения задачи следует произвести две последовательные замены плоскостей проекций. В результате первой замены одна из прямых должна оказаться параллельной новой плоскости проекций, а после второй замены эта прямая должна стать перпендикулярной следующей вводимой плоскости проекций.

На рис. 5.5 заменим, например, плоскость V плоскостью V₁, параллельной прямой АВ. Новую ось Х₁ проводим параллельно ab и строим новые проекции a₁^′b₁′ и c₁'d₁'. Затем плоскость Н заменяем плоскостью Н₁, перпендикулярной к прямой АВ, располагая новую ось Х₂ перпендикулярно a₁′b₁′. При этом прямая АВ спроецируется на плоскость Н₁ в точку a₁≡b₁.

Отрезок MN располагается параллельно плоскости Н₁ и определяет искомое расстояние.

При помощи линий проекционной связи, проводимых в обратном направлении, находим проекции тп и т'п′ этого отрезка на исходных плоскостях проекций Н и V.

Задача 5. Определить величину двугранного угла при ребре АВ (рис. 5.6).

Двугранный угол измеряется линейным углом, образованным линиями пересечения его граней плоскостью, которая перпендикулярна к ним. Он проецируется в натуральную величину на плоскость, перпендикулярную к его ребру.

Для решения задачи:

1. Заменим плоскость V плоскостью V₁ таким образом, чтобы общее ребро АВ превратилось в прямую уровня.

2. Заменим плоскость Н плоскостью Н₁ так, чтобы общее ребро АВ заняло проецирующее положение.

3.Получаем линейный угол φ₁, определяющий величину заданного двугранного угла.

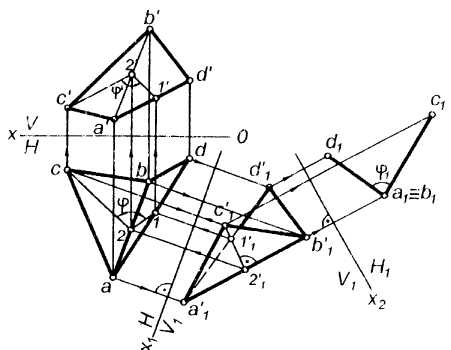4. Находим проекции φ и φ′ этого угла на исходных плоскостях Н и V при помощи линий проекционной связи, проводимых в обратном направлении.

Рис. 5.6