Задача 1. Определить расстояние от точки 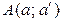 до прямой
до прямой 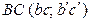 (рис. 85).
(рис. 85).
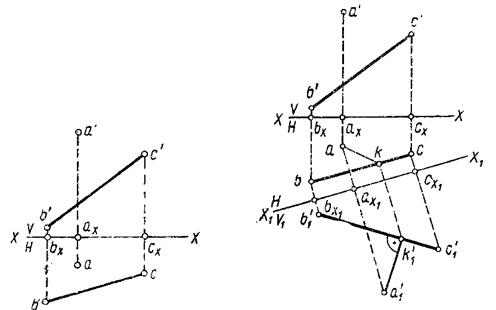
Рис. 85 Рис. 86
Ре ш е н и е. Расстояние от точки до прямой выражается отрезком перпендикуляра, опущенного из данной точки на данную прямую и ограниченного данной точкой и точкой его пересечения с прямой, т.е. необходимо прежде всего опустить из точка 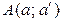 на прямую
на прямую 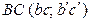 перпендикуляр и найти его основание.
перпендикуляр и найти его основание.
Прямой угол между данной прямой ВС и прямой к ней перпендикулярной, будет проектироваться без искажения на плоскость, параллельную данной прямой. Следовательно, прежде всего необходимо выбрать новую плоскость проекций, параллельную прямой 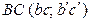 : выбираем новую плоскость
: выбираем новую плоскость 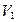 , параллельную прямой ВС, такому выбору плоскости на ортогональном чертеже (рис. 86) соответствует выбор новой оси
, параллельную прямой ВС, такому выбору плоскости на ортогональном чертеже (рис. 86) соответствует выбор новой оси 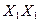 параллельно проекции
параллельно проекции 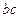 .
.
Строим на новой плоскости проекций 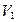 проекции точки
проекции точки 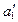 и проекцию прямой
и проекцию прямой 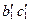 . Затем из точки
. Затем из точки 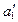 на проекцию прямой
на проекцию прямой 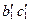 опускаем перпендикуляр и находим его основание
опускаем перпендикуляр и находим его основание 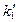 –– точка
–– точка 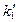 является проекцией на плоскость
является проекцией на плоскость 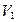 основания перпендикуляра
основания перпендикуляра 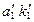 , опущенного из данной точки на данную прямую.
, опущенного из данной точки на данную прямую.
Для построения проекции на плоскость Н этого перпендикуляра 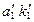 , через точку
, через точку 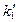 проводим прямую, перпендикулярную к оси
проводим прямую, перпендикулярную к оси 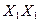 (линию проекционной связи) до пересечения в точке
(линию проекционной связи) до пересечения в точке 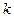 с проекцией bc, и точку а соединяем с точкой
с проекцией bc, и точку а соединяем с точкой 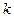 (рис. 86).
(рис. 86).
Отрезки 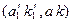 являются проекциями расстояний от данной точки А до заданной прямой ВС соответственно в плоскостях проекций
являются проекциями расстояний от данной точки А до заданной прямой ВС соответственно в плоскостях проекций 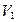 и Н, но это ещё не истинное расстояния от точки А до прямой ВС, а только её проекции.
и Н, но это ещё не истинное расстояния от точки А до прямой ВС, а только её проекции.
Последним этапом решения задачи является определение истинной длины отрезка 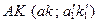 , который является искомым расстоянием. Указанный отрезок будет проектироваться без искажения на плоскость ему параллельную. Следовательно, для окончательного решения задачи необходимо выбрать новую плоскость проекций
, который является искомым расстоянием. Указанный отрезок будет проектироваться без искажения на плоскость ему параллельную. Следовательно, для окончательного решения задачи необходимо выбрать новую плоскость проекций 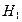 , параллельную отрезку
, параллельную отрезку 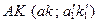 (рис. 87).
(рис. 87).
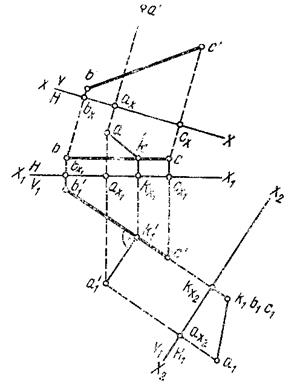
Рис. 87
В качестве новой плоскости проекций выбираем плоскость 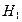 На ортогональном чертеже выбору этой плоскости соответствует выбор новой оси
На ортогональном чертеже выбору этой плоскости соответствует выбор новой оси 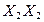 параллельно проекции
параллельно проекции  [6]. Построенную новую систему плоскостей проекций
[6]. Построенную новую систему плоскостей проекций 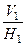 с осью
с осью 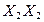 свяжем на ортогональном чертеже рисунка 85 с системами
свяжем на ортогональном чертеже рисунка 85 с системами 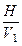 и
и 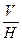 .
.
Строим в плоскости 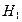 системы
системы 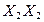 проекцию отрезка
проекцию отрезка 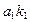 , откладывая для получения проекции каждой точки этого отрезка соответственно расстояния от оси
, откладывая для получения проекции каждой точки этого отрезка соответственно расстояния от оси 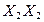 : для получения точки
: для получения точки 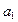 –
– 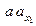 , а для точки
, а для точки 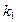 –
– 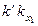 . Нужно отметить, что проекция (
. Нужно отметить, что проекция (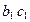 ) прямой ВС на плоскости проекций
) прямой ВС на плоскости проекций 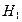 проектируется в точку, совпадая с проекцией
проектируется в точку, совпадая с проекцией 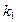 , т.к. в пространстве плоскость
, т.к. в пространстве плоскость 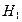 перпендикулярна к прямой ВС (см. рис. 87).
перпендикулярна к прямой ВС (см. рис. 87).
Длина проекции 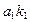 является истинной длиной расстояния от точки А до прямой ВС –– задача решена.
является истинной длиной расстояния от точки А до прямой ВС –– задача решена.
 2017-10-25
2017-10-25 917
917








