Из совокупности студентов произведены две 20%-ые выборки для изучения оценки.
Известны следующие данные об успеваемости студентов:
| Оценка | Генеральная совокупность | Выборочные совокупности | |
| первая | вторая | ||
| итого |
Средняя в генеральной совокупности равна:
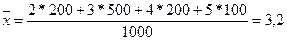
Доля отличников:
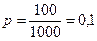
По данным первой выборки выборочная средняя и доля равны:
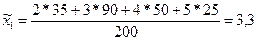

По данным второй выборки выборочная средняя и доля равны:
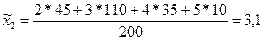
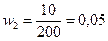
Выделяют:
1) ошибку средней 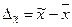
- для первой выборки 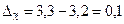
- для второй выборки 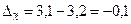
2) ошибку доли 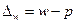
- для первой выборки 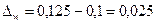
- для второй выборки 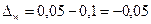
Таким образом, можно сделать вывод, что ошибки выборки являются переменными величинами и могут принимать различные значения. Поэтому рассчитывают среднюю из возможных ошибок μ.
Математически доказано, что например при случайном повторном отборе средняя ошибка определяется по следующей формуле:
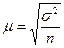 и т.д.
и т.д.
Но ошибка конкретной выборки может оказаться выше средней ошибки, поэтому рассчитывают предельную ошибку выборки:
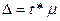 , где t – коэффициент доверия, который определяется по таблице значений интегральной функции Лапласа при заданной доверительной вероятности P, выдержки из которой приведены ниже
, где t – коэффициент доверия, который определяется по таблице значений интегральной функции Лапласа при заданной доверительной вероятности P, выдержки из которой приведены ниже
 2015-04-12
2015-04-12 351
351








