2015-04-12
211
Уравнение регрессии выражает ср. вел-ну рез. признака как ф-цию факт. признака.
Уравнение регрессии в общем виде: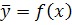 
Уравнение регрессии – линия, вокруг кот. группируются точки корр. поля.
Прежде чем определить уравнение регрессии нужно определить его форму (линейная, парабола, гипербола, логарифм). Чаще всего используется линейная форма связи (для парной корреляции (1 рез. и 1 факт)):
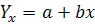
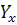– теор. зна-ние рез. приз-ка; 
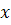– факт. признак; 
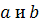– параметры ур. регрессии.
Чаще эти параметры ищут испо-зуя метод наименьших квадратов: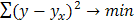 
Для линейн. формы: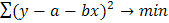 
Далее получаем следующую систему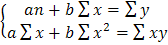 
Проверка правильности расчета. Для этого в ур. подставляют вместо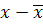 
, вместо 
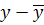(средняя).
Если получается тождество, то уравнение рассчи-но верно.
Основные показатели теснотысвязи между признаками:
1) линейный коэффициент корреляции
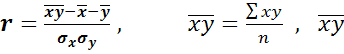– среднее из произведений
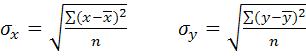
среднеквадратичное отклонение факт. признаков
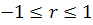Чем ближе к 1 или -1, тем теснее связь между признаками.
2) эмпирическое коррел. отношение (см.тему ср. величины)
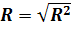
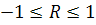
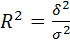(коэф. детерминации), 
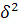– межгруппов. дисперсия, 
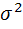- общая дисперсия
Чем ближе к 1 или -1, тем теснее связь между признаками.
3) коэффициент рангов Спирмена
Каждой единице совокупности в порядке возраст. значений присваивают номер, кот. наз-ют рангом.
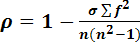f – разность. рез. и факт. признаков (вариант и частот)
