 Ранее было показано, что в результате действия момента внешней силы главная ось гироскопа перемещается относительно первоначального положения.
Ранее было показано, что в результате действия момента внешней силы главная ось гироскопа перемещается относительно первоначального положения.
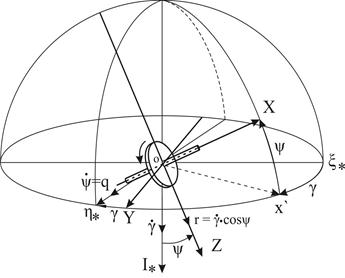
Следовательно, можно сказать, что в общем случае гироскоп изменяет свое положение относительно инерциального пространства и земных плоскостей, т.е. сферические координаты осей гироскопа непрерывно изменяется, для определения положения гироскопа достаточно знать положение его главной оси Х. Возьмем ИСК и мгновенное положение главной оси Х гироскопа в этой системе координат. Тем самым будет определено положение осей Y и Z гироскопа (рис.7). На рис.7 показано положение главной оси X
Рис.7 гироскопа, отклоненной на углы γ и ψ
Из рис. 7 видно, что угловая скорость вращения гироскопа вокруг оси I* ИСК определится вектором 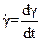 ,а вокруг оси Y гироскопа - вектором
,а вокруг оси Y гироскопа - вектором 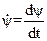 .Тогда угловая скорость вращения гироскопа вокруг оси Z гироскопа определится вектором r = γ·cosψ.
.Тогда угловая скорость вращения гироскопа вокруг оси Z гироскопа определится вектором r = γ·cosψ.
Для определения сферических координат положения гироскопа в инерциальном пространстве γ и ψ необходимо знать законы движения главной оси X гироскопа вокруг осей X Y и Z. Эти законы могут быть найдены из технических уравнений движения гироскопа. Технические уравнения, или усеченные уравнения Эйлера, имеют вид:
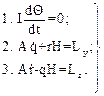 (11)
(11)
где: I и А – полярный и экваториальный моменты инерции соответственно; 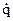 и
и 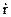 – абсолютные (относительно ИСК) угловые скорости движения главной оси гироскопа вокруг осей У и Z; Ly и Lz –моменты внешних сил, действующих вокруг осей У и Z соответственно.
– абсолютные (относительно ИСК) угловые скорости движения главной оси гироскопа вокруг осей У и Z; Ly и Lz –моменты внешних сил, действующих вокруг осей У и Z соответственно.
Уравнение 1 – системы определяет постоянную угловую скорость собственного вращения гироскопа, поэтому в дальнейшем оно рассматриваться не будет.
Уравнения 2 и 3 системы характеризуют величины моментов внешних сия, действующих по осям У и Z гироскопа соответственно, или проекции моментов на указанные оси. Первые слагаемые левых частей уравнений (11) называются инерциальными членами, вторые слагаемые – гироскопическими членами технических уравнений движения гироскопа.
Анализ уравнений (11) показывает, что угловые скорости абсолютного движения q и r гироскопа можно определить по значениям моментов внешних сил Ly и Lz. Рассчитав значения q и r, можно определить сферические координаты положения главной оси Х гироскопа в ИСК, т.е. углы γ и ψ. Чтобы найти углы γ и ψ, необходимо знать угловые скорости 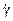 и
и 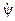 . Из рис.7 видно, что указанные скорости связаны следующими соотношениями:
. Из рис.7 видно, что указанные скорости связаны следующими соотношениями:

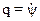 ;(12)
;(12)
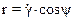 (13)
(13)
 2015-04-12
2015-04-12 2769
2769
