АВЛ-деревья

Можно ли при работе с бинарными деревьями поиска гарантировать оценку T(n) = O(log(n)) для поиска и вставки не только в среднем, но и в худшем случае? Ответ положительный. Однако для этого следует выбрать подходящий класс деревьев. Для произвольных бинарных деревьев операция вставки выполняется просто и быстро, но поиск может быть долгим в случае вырождения. ИС-деревья гарантируют быстрый поиск, но много времени уходит на поддержание баланса при вставке и удалении. Желательно найти какой-то «средний» тип деревьев, чтобы они были не намного хуже, чем идеально сбалансированные, но вставка выполнялась значительно быстрее.

Было предложено несколько подобных типов деревьев. Среди них АВЛ-деревья [1, 5], 2-3-деревья [3, 5], красно-черные деревья [4]. Мы рассмотрим только АВЛ-деревья, которые были названы в честь предложивших их советских математиков Г.М.Адельсона-Вельского и Е.М.Ландиса и которые до настоящего времени остаются одним из лучших средств решения задачи поиска со вставкой.

АВЛ-деревом [3] называется такое бинарное дерево поиска, для каждой вершины которого высота ее левого и правого поддеревьев отличаются не более, чем на единицу.

Легко видеть, что всякое ИС-дерево поиска является АВЛ-деревом. Обратное, вообще говоря, неверно.

На рис. 4.3 показаны примеры самых худших (т.е. наиболее разбалансированных, «перекошенных») АВЛ-деревьев для различных значений высоты. Как видно из рисунка, даже в худшем случае АВЛ-деревья далеки от вырожденности. Это становится все более заметно при увеличении высоты. Можно доказать, что высота АВЛ-дерева превышает высоту ИС-дерева с тем же количеством вершин не более, чем на 45 %. Таким образом, логарифмическая зависимость высоты от числа вершин сохраняется даже в худшем случае.

Таким образом, качество АВЛ-деревьев вполне приемлемо для быстрого поиска. Покажем, что поддержание сбалансированности при вставке новой вершины для этого типа деревьев требует лишь нескольких операций с указателями.

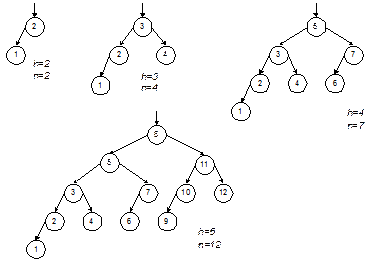
Рис. 4.3. Наихудшие АВЛ-деревья разной высоты

Прежде всего, надо выяснить, каким образом вообще обнаруживается нарушение сбалансированности при вставке. Наиболее удобное решение – хранить в каждой вершине АВЛ-дерева дополнительное поле bal (баланс), которое может принимать одно из трех значений:

t^.bal = –1, если левое поддерево вершины t выше, чем правое;

t^.bal = 0, если оба поддерева одинаковы по высоте;

t^.bal = +1, если правое поддерево t выше, чем левое.

При выполнении вставки сначала происходит рекурсивный спуск по дереву, затем новая вершина добавляется как лист (и для нее, естественно, устанавливается начальное значение bal = 0), а затем, в процессе возврата вверх, для всех вершин соответствующей ветви дерева выполняется корректировка значений поля bal, если вставка новой вершины вызвала увеличение высоты левого или правого поддерева.

Пусть при возврате вверх после вставки выяснилось, что для некоторой вершины C баланс нарушен: левое поддерево C теперь оказалось на 2 единицы выше, чем правое (случай перекоса вправо рассматривается аналогично). При этом для вершин, лежащих ниже C, баланс остается в пределах нормы (от –1 до +1). В этой ситуации возможны два существенно разных случая, проиллюстрированных на рис. 4.4.

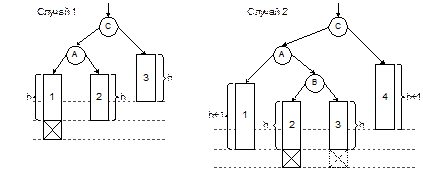
Рис. 4.4. Нарушение баланса при вставке в АВЛ-дерево

Буквой A обозначен левый сын вершины C. Высота поддерева A могла увеличиться либо при вставке в левое поддерево A (случай 1), либо при вставке в правое поддерево (случай 2). Прямоугольники 1, 2, 3, 4 обозначают поддеревья произвольной сложности, а перечеркнутый квадрат – добавленную вершину. Во втором случае показаны два возможных положения добавленной вершины, одно из них – пунктиром. Можно доказать, что в случае 1 высоты поддеревьев 1, 2 и 3 равны одной и той же величине h, а в случае 2 высоты поддеревьев 1 и 4 на единицу больше, чем 2 и 3.

Для восстановления баланса изображенные части дерева должны быть переставлены так, как показано на рис. 4.5.

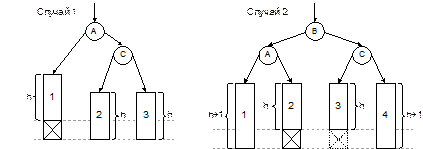
Рис. 4.5. Восстановление баланса АВЛ-дерева

Такие преобразования АВЛ-дерева принято называть его поворотами.

Прежде всего заметим, что повороты не нарушают упорядоченность дерева поиска (например, в случае 1 и до поворота, и после него ключи в различных частях дерева упорядочены следующим образом: 1 £ A £ 2 £ C £ 3). При этом восстанавливается баланс вершин дерева.

Преобразования поворота выполняются с помощью нескольких присваиваний значений указателей. Ниже приведен в качестве примера фрагмент программы, выполняющий поворот для случая 1.

var

t: Tree; {Корень поворачиваемой части дерева}

p: Tree; {Рабочая переменная}

...

p:= t^.left; {p -> A}

t^.left:= p^.right; {C -> 2}

p^.right:= t; {A -> C}

t^.bal:= 0; {Оба поддерева C стали одной высоты}

t:= p; {A – новый корень повернутой части}

t^.bal:= 0; {Оба поддерева A тоже одной высоты}

...

Из сравнения рис. 4.4 и 4.5 можно заметить, что высота рассматриваемой части дерева не увеличивается после вставки и последующего поворота. Это значит, что баланс вышележащих вершин дерева не изменяется и эти вершины не потребуют дополнительных поворотов.