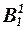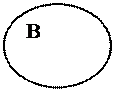
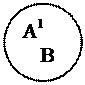

 1 случай: 2 случай:
1 случай: 2 случай:
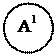 "А1(x)В(x) и "А1(x)В(x) и
"А1(x)В(x) и "А1(x)В(x) и
$А1(x)В(x) и $А1(x)В(x) и



 3случай: 4 случай:
3случай: 4 случай:
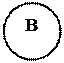
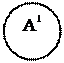
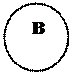
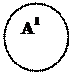 "А1(x)В(x) л "А1(x)В(x) л
"А1(x)В(x) л "А1(x)В(x) л
$А1(x)В(x) л $А1(x)В(x) и
 | |||
 |
5 случай:
 "А1(x)В(x) л
"А1(x)В(x) л
$А1(x)В(x) и
.
Правила ПС.3.1–ПС.3.3, ПС.3.4.", ПС.3.5.$ задают смыслы функторов ЯЛФРТ. Каковы предметные значения (денотаты) этих функторов? В некоторых случаях функции, выражаемые функторами, рассматриваются как абстрактные предметы, обозначаемые этими функторами; однако в большинстве ЯЛФРТ функторы рассматриваются как выражения, не имеющие денотатов; такие выражения называются синкатегорематическими, в отличие от категорематическиx выражений, то есть выражений, имеющих не только смысловое, но и предметное значение.
Абстрактор – это сложный функтор ЯЛФРТ, переводящий путем связывания пустого места предикатор (оператор) в имя абстрактного предмета, полученного из предиката (операции), выражаемого этим предикатором (оператором), с помощью особого логического действия – абстракции. В естественном языке абстрактор выражается словами: «свойство», «отношение», «признак» и т.д., например, выражение естественного языка «свойство быть красным» («краснота») представляется в ЯЛФРТ как результат действия абстрактора «свойство …, такое что [+++]» на предикатор «… (есть) красный». Выражение ЯЛФРТ «свойство …, такое что [… (есть) красный]» является именем абстрактного предмета – красноты; вхождение пустого места «…» в это выражение является связанным.
Классообразователь (функтор множества) – сложный функтор ЯЛФРТ, переводящий путем связывания пустого места предикатор в имя абстрактного предмета – класса или множества. В естественном языке классообразователь выражается словами «множество» или «класс». Выражение естественного языка «множество людей» в ЯЛФРТ представляется как результат действия классообразователя «множество (класс) … таких что [+++]» на предикатор «… (есть) человек». Выражение ЯЛФРТ «множество (класс) …, такое что [… (есть) человек]» является именем абстрактного предмета – множества (класса) людей.
Для того, чтобы определить смыслы абстрактора и классообразователя, необходимо ввести в рассмотрение особое логическое действие – абстракцию. Под абстракцией в логике понимают логическое действие, при котором некоторая функция (предикат, операция) рассматривается как особый предмет – абстрактный предмет. Дело в том, что в семантике ЯЛФРТ имеют дело с двумя видами «сущностей»: предметами, то есть денотатами имен, и функциями, то есть смыслами функторов. Предметы в общем случае не являются функциями, а функции не являются предметами. Абстракция в логике как раз и понимается как переход к новой предметной области, предметами которой являются функции, определенные на исходной предметной области. Абстрактор и классообразователь входят в состав правильно построенных термов ЯЛФРТ. Фундаментальное индуктивное определение ППТ дополняется теперь новым пунктом:
(4i) (индукционный шаг) если Fn – n-местная операторная (функциональная) константа, Аn – n-местная предикатная константа, x, x1, x2, … xn – индивидные переменные (n=1,2,…), l – знак абстрактора, {½ } – знак классообразователя, то выражения вида: lxФ1(x), lxА1(x), lx1,x2,...,xnФn(x1, x2 ,…,xn), lx1,x2,...,xnАn(x1, x2 ,…,xn), {x½А1(x)}, {áx1, x2,..., xnñ½Аn(x1, x2,..., xn)} – ППТ (символы абстрактора, классообразователя, скобки, запятые употреблены автонимно).
Смыслы ППТ и ППФ, содержащих символ абстрактора, задается следующим семантическим правилом.
ПС3.6. (i) Выражение lxФ1(x) обозначает одноместную операцию, определенную на области изменения переменной х, рассматриваемую как особый абстрактный предмет, то есть предмет, полученный из функции (операции) с помощью логического действия абстракции.
(ii) Выражение lx1,x2,...,xnФn(x1, x2 ,…,xn) обозначает n-местную операцию, определенную на области упорядоченных n-ок предметов, взятых из областей изменения переменных x1, x2,…,xn в соответствующем порядке, рассматриваемую как особый абстрактный предмет.
(iii) Выражение lxA1(x) обозначает одноместный предикат, определенный на области изменения переменной х, рассматриваемый как особый абстрактный предмет.
(iv) Выражение lx1,x2,...,xnАn(x1, x2 ,…,xn) обозначает n-местный предикат, определенный на области упорядоченных n-ок предметов, взятых из областей изменения переменных x1, x2,…,xn в соответствующем порядке, рассматриваемый как особый абстрактный предмет.
Пример 2.10. На предметной области конкретныx предметов (то есть предметов, доступных чувственному восприятию, существующих в пространстве и времени) определяются конкретные предикаты: «x –красный», «x – синий», «x – зеленый», «x – твердый», «x – горький».
ОО: конкретные предметы

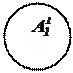
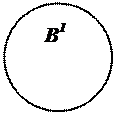 x – красный А1(x)
x – красный А1(x)
 x – синий В1(x)
x – синий В1(x)

 x – твердый
x – твердый  (x)
(x)
|
 (x)
(x)
 | |||
 | |||
ОО: свойства конкретных предметов x – цвет А1(x)
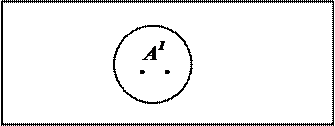

 ..
..
l x (x – красный)  l x (x – синий)
l x (x – синий)
Действуя абстрактором l x (...) на предикаторы А1(x) –  (x), получаем имена предметов новой предметной области – области абстрактных предметов, предметами которой являются свойства конкретных предметов, рассматриваемые как особые предметы: l x (x –красный) – «свойство быть красным», «краснота»;l x (x –синий) – «синева»; l x (x –твердый) – «твердость»; l x (x –горький) – «горечь». На новой предметной области абстрактных предметов определяются новые предикаты – абстрактные предикаты (абстрактные понятия), например, предикат «x – цвет».
(x), получаем имена предметов новой предметной области – области абстрактных предметов, предметами которой являются свойства конкретных предметов, рассматриваемые как особые предметы: l x (x –красный) – «свойство быть красным», «краснота»;l x (x –синий) – «синева»; l x (x –твердый) – «твердость»; l x (x –горький) – «горечь». На новой предметной области абстрактных предметов определяются новые предикаты – абстрактные предикаты (абстрактные понятия), например, предикат «x – цвет».
Терминология любой науки, использующей аппарат современной логики, содержит термины (понятия) различных уровней абстракции. Уровень абстракции научной терминологии определяется индуктивно:
1) 0-ой (нулевой) уровень абстракции (уровень абстракции с порядковым номером 0) составляют конкретные предикаты (понятия);
2) n+1-ый (n плюс первый) уровень абстракции (уровень абстракции с порядковым номером n+1) составляют понятия (предикаты), область определения которых состоит из абстрактных предметов, полученных путем абстракции из понятий n-ого уровня абстракции, или кортежей этих абстрактных предметов;
3) каждый термин научной терминологии относится к одному и только одному уровню абстракции.
Определенное выше логическое действие называется также абстракцией отождествления, поскольку в основе этого действия лежит отождествление предметов (или кортежей предметов) по общему для них свойству (отношению). При образовании абстрактных предметов в науках, использующих аппарат современной логики, применяют также так называемые идеализирующие абстракции; с помощью таких абстракций вводятся так называемые идеальные или идеализированные объекты, то есть объекты, фиксирующие свойства, заведомо отсутствующие у конкретных объектов («идеальный газ», «идеальная паровая машина» и т. д.). Наиболее употребительными в математике являются абстракция потенциальной осуществимости, с помощью которой образуется потенциально бесконечный ряд натуральных чисел (мы отвлекаемся здесь от ограниченности материальных возможностей построения конкретных совокупностей материальных предметов, содержащих любое число членов), и абстракция абсолютной осуществимости, согласно которой в логике признается существующим любой абстрактный предмет с непротиворечивыми свойствами; с помощью данной абстракции в математике при рассуждениях о потенциально бесконечных последовательностях используются в полном объеме законы классической логики (в частности, законы непротиворечия и исключенного третьего), что равнозначно рассмотрению таких принципиально незавершенных конструкций как законченных, данных всеми своими членами одновременно.
С понятием абстракции тесно связан важнейший принцип дидактики – принцип наглядности обучения. В отношении терминологии изучаемой научной дисциплины суть этого принципа может быть выражена следующим образом: в процессе преподавания любой научной дисциплины все термины должны вводится последовательно, начиная с нулевого уровня абстракции; при переxоде к понятиям более высокого уровня абстракции необxодимо фиксировать внимание учащиxся на используемыx при этом абстракцияx; учащийся должен уметь сводить понятия любого уровня абстракции к конкретным понятиям, то есть понятиям нулевого уровня абстракции.
Смысл классообразователя (функтора множества)задается следующим семантическим правилом.
ПС3.7. (i) Выражение {x½А1(x)} обозначает область истинности предиката А1(x), рассматриваемую как особый абстрактный предмет, – множество (класс)предметов из области изменения переменной х, обладающих свойством А1(x).
(ii) Выражение {áx1, x2,..., xnñ½Аn(x1, x2,..., xn)} обозначает область истинности предиката Аn(x1, x2,..., xn), рассматриваемую как особый абстрактный предмет – множество (класс)упорядоченных n-ок предметов из области определения предиката Аn(x1,x2,...,xn), находящихся в отношении Аn(x1,x2,..., xn).
Логическое действие, при котором область истинности некоторого предиката рассматривается как особый абстрактный предмет, называется в логике экстенсиональнойабстракцией (от латинского extendo – растягивать, распространять, расширять); в классической логике области истинности предиката, рассматриваемой как абстрактный предмет – множество или класс, соответствует объем понятия.
Пример 2.11. Выражение { x ½ x –отец} обозначает абстрактный предмет – «множество (класс) всех отцов», то есть область истинности предиката «x –отец», рассматриваемую как особый абстрактный предмет. Выражение {á x1, x2 ñ½ x1 отец x2 } обозначает абстрактный предмет – «множество (класс) всех пар людей á x1, x2 ñ, таких что x1 есть отец x2».
В соответствии с ранее принятым соглашением мы будем в дальнейшем использовать сокращения: вместо {x½А1(x)} будем писать А1, и вместо {áx1, x2,..., xnñ½Аn(x1, x2,..., xn)} будем писать Аn.
Пример 2.12. В теоретико-множественной математике натуральные числа рассматриваются как множества, то есть вводятся с помощью экстенсиональной абстракции.
Нулевой уровень абстракции:
ОО: конкретные предметы
 x (есть) один 11(x)
x (есть) один 11(x)
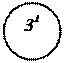 x (есть) два 21(x)
x (есть) два 21(x)
x (есть) три 31(x)
...
Путем экстенсиональной абстракции образуем множества { x ½ 11(x) } или 11, { x ½ 21(x) } или 21, { x ½ 31(x) } или 31 и т. д. Эти множества образуют начальный отрезок натурального ряда чисел: 1, 2, 3,.... Определив на новой предметной области операцию «x +1» или «следующий за x», с помощью абстракции потенциальной осуществимости получаем потенциально бесконечный натуральный ряд чисел, на котором могут быть определены абстрактные понятия: «x –четное число», «x – нечетное число» и т. д.
Первый уровень абстракции
ОО: конечные множества
конкретных предметов
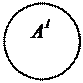 x – четное число А1(x)
x – четное число А1(x)
|
Отношение принадлежности элемента множеству – исходное отношение теории множеств,обозначается: а Î {x½А1(x)}, читается: «предмет а принадлежит множеству {x½А1(x)}, является элементом множества {x½А1(x)}», или
áа1, а2,..., аnñ Î {áx1, x2,..., xnñ½Аn(x1, x2,..., xn)},
читается: «кортеж предметов áа1, а2,..., аnñ принадлежит множеству {áx1, x2,..., xnñ½Аn(x1, x2,..., xn)}, является элементом множества {áx1, x2,..., xnñ½Аn(x1, x2,..., xn)}», – определяется следующим образом:
а Î {x½А1(x)}, если и только если А1(а) – истинно, то есть если и только если предикат А1(x) ставит в соответствие предмету а значение и (то есть предмет а обладает свойством А1(x), предмет а попадает в область истинности предиката А1(x));
áа1, а2,..., аnñ Î {áx1, x2,..., xnñ½Аn(x1, x2,..., xn)}, если и только если Аn(x1, x2,..., xn) – истинно, то есть если и только если предикат Аn(x1, x2,..., xn) ставит в соответствие кортежу áа1, а2,..., аnñ значение и (то есть предметы а1, а2,..., аn находятся в отношении Аn(x1, x2,..., xn), кортеж áа1, а2,..., аnñ попадает в область истинности предиката Аn(x1, x2,..., xn)).
Множество {áx1, x2,..., xnñ½Аn(x1, x2,..., xn)} (сокращенно Аn) равномножеству {áx1, x2,..., xnñ½Вn(x1, x2,..., xn)} (сокращенно Вn), если и только если они включают одни и те же элементы, то есть каждый элемент множества Аn принадлежит Вn и каждый элемент множества Вn принадлежит Аn. Равенство множеств записывается с помощью символа равенства =:
{áx1, x2,..., xnñ½Аn(x1,x2,..., xn)} = {áx1, x2,..., xnñ½Вn(x1,x2,..., xn)}
или Аn = Вn.
Множество Аn является подмножеством множества Вn:
Аn Í Вn , если и только если каждый элемент Аn является элементом Вn.
Множество Аn является собственным подмножествоммножества Вn: Аn Ì Вn, если и только если каждый элемент Аn является элементом Вn и существуют элементы Вn, которые не являются элементами Аn.
Отношения между множествами графически представлено схемой 2.6.
 2015-04-01
2015-04-01 654
654