Схема 2.4

с р А И

х у z В

авЛ

И

Л

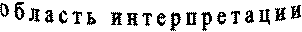Вторым важнейшим семантическим понятием языков логики является понятие функции.

Под функцией в логике понимают много-однозначное или одно-однозначное соответствие между двумя областями, первая из которых называется областью определения функции (ОО), а вторая – областью значений функции (ОЗ). Область определения функции состоит из элементов: предметов или упорядоченных n-ок предметов (n=2,3,4, …), называемых также кортежами или n-членными последовательностями; в первом случае функция называется одноместной или одноаргументной, а во втором – n-местной или n-аргументной (n=2,3,4, …). Функция каждому элементу из ОО ставит в соответствие один и только один предмет из ОЗ, но при много-однозначном соответствии различным элементам из ОО может ставиться в соответствие одини тот же предмет из ОЗ, а при одно-однозначном соответствии различным элементам из ОО ставятся в соответствие различные предметы из ОЗ. Область значений функции в обоих случаях включает в себя предметы. Если не всем элементам из ОО ставятся в соответствие предметы из ОЗ, то такое соответствие называется частичной функцией (из ОО в ОЗ). Упорядоченную n-ку предметов (n=2,3,4, …) мы будем обозначать с помощью угловых скобок: áа₁, а₂, …,а_nñ – упорядоченная n-ка (n-членный кортеж) предметов, называемых именами а₁, а₂, …,а_n. Две упорядоченные n-ки предметов áа₁, а₂, …,а_nñ и áb₁, b₂, …,b_mñ равны друг другу (представляют собой одну и ту же упорядоченную n-ку предметов): áа₁, а₂, …,а_nñ = áb₁, b₂, …,b_mñ, если и только если: (1) n=m; (2) а_i и b_i называют один и тот же предмет, что выражается с помощью знака логического равенства: a_i = b_i(1 £ i £ n).

Говорят, что функция определена на данной предметной области, если и только если ее область определения содержит предметы из данной предметной области или упорядоченные n-ки предметов из данной предметной области.

Введенное здесь понятие функции позволяет сформулировать семантические правила, приписывающие смысловые значения выражениям ЯЛФРТ, относящимся к семантической категории функторов (то есть включающим в свой состав переменные). При интерпретации ЯЛФРТ функции, определенные на области интерпретации, сопоставляются функторам данного ЯЛФРТ (то есть выражениям, содержащим в своем составе переменные) как их смысловые значения.

ПС.3. (Правило семантическое третье). Функтор выражает функцию.

Пример 2.4. Функтор «отец …» (пустое место замещается именами людей) выражает функцию:

ОО (область определения) ОЗ (область значений)

люди за весь период их жизнилюди за весь период их жизни

а а

Елизавета Петровна · ·

Романова

b b

Алексей Михайлович · ·

Романов

cc

Петр I · ·

a₁ a₁

Михаил Романов · ·

Согласно определению, функция ставит в соответствие каждому человеку из ОО другого человека из ОЗ – его отца, причем каждому человеку из ОО ставится в соответствие один и только один человек (его отец) из ОЗ, и нескольким людям из ОО может быть поставлен в соответствие один и тот же человек из ОЗ, но не наоборот (много-однозначное соответствие).

При интерпретации операторным и предикатным константам, а также символам коннекторов сопоставляются функции, определенные на универсуме рассуждения (области интерпретации), а для операторных и предикатных переменных указываются области их изменения – то есть области, содержащие функции, определенные на области интерпретации.

ПС.3.1. Элементарный постоянный оператор,содержащий единственную n-местную операторную константу (n=1,2,3,...), в заданнойинтерпретации выражаетоперацию, то есть функцию, областью определения (ОО) которой является подобластьобласти интерпретации, не содержащая { и, л }, – при n=1; или область, состоящая из упорядоченных n-ок (n-членных последовательностей, кортежей) предметов из этой подобласти, – при n=2,3,...; а областью значений (ОЗ) – та же самая или другая подобластьобласти интерпретации, не содержащая { и, л }. Элементарный переменный оператор,содержащий n-местную операторную переменную, принимает значения в (пробегает по) области n-местных операций, определенных на области интерпретации.

Элементарный постоянный оператор отец¹(х) (операторная константа отец¹ интерпретируется как операция, выражаемая оператором «отец …»из примера 2.4, х пробегает по области людей) выражает операцию, описанную в примере 2.4.

Пример 2.5. Оператор +²(х,у) (+² интерпретируется как «… + _***»; x, у пробегают по области натуральных чисел) выражает двуместную операцию сложения натуральных чисел, то есть функцию:

ОО ОЗ

упорядоченные двойки натуральные числа

натуральных чисел

á1,2ñ · · 3

á2,7ñ ·

á3,5ñ · · 8

á5,3ñ · · 9

ПС.3.2. Элементарный n-местныйпостоянный предикатор в заданной интерпретациивыражает n-местныйпредикат (пропозициональную функцию), то есть функцию, ОО которой является подобласть области интерпретации, не содержащая { и, л }, – при n=1, или область, состоящая из упорядоченных n-ок (n-членных последовательностей, кортежей) предметов из этой подобласти, – при n=2,3,..., а ОЗ – { и, л }. Элементарный n-местныйпеременный предикатор пробегает по (принимает значение в) области n-местных предикатов, определенных на области интерпретации.

Пример 2.6. Предикатор А¹(х) (А¹ интерпретируется как «…(есть) отец»; x пробегает по области людей, то есть по той же области, что и в примере 2.4) выражает предикат:

ОО ОЗ

люди { и, л }

а

Елизавета Петровна ·

Романова

b и

Алексей Михайлович · ·

Романов л

c ·

Петр I ·

a₁

Михаил Романов ·

Пример 2.7. Предикатор А²(х,у) (А² интерпретируется как «…(есть) отец _{* * *}»; x, у пробегают по области людей, то есть по той же области, что и в примерах 2.4, 2.6) выражает предикат:

ОО ОЗ

упорядоченные пары людей { и, л }

á с, а ñ ·

á а, с ñ · · и

á с, b ñ · · л

á a, b ñ ·

á a, a ñ ·

В современной логике вводится понятие 0-местного функтора и 0-местной функции. 0-местная функциональная константа обозначает предмет из универсума рассуждений; 0-местная функциональная переменная совпадает с индивидной переменной. 0-местная предикатная константа совпадает с пропозициональной константой, 0-местный предикат оказывается одним из двух абстрактных предметов – и или л; 0-местная предикатная переменная совпадает с пропозициональной переменной.

Каждый предикат разбивает область своего определения на две области: область истинности предиката, то есть область, состоящую из тех элементов ОО предиката, которым предикат ставит в соответствие и, и область ложности предиката, то есть область, состоящую из тех элементов ОО предиката, которым предикат ставит в соответствие л.

Предикаты в современной логике отождествляются с понятиями в традиционной логике, то есть с мыслями о свойствах предметов и отношениях между ними (с мыслями о признаках предметов). Понятия-свойства отождествляются с одноместными предикатами и выражаются одноместными предикаторами, а понятия-отношения отождествляются с многоместными предикатами и выражаются многоместными предикаторами.

Графический язык представления предикатов

ОО предиката изображается прямоугольником, каждая точка которого представляет элемент (предмет или кортеж предметов) ОО предиката, а область истинности предиката изображается кругом, внутренние точки которого представляют элементы, которым предикат ставит в соответствие и.

Предикаты из примеров 2.6. и 2.7. графически представляются следующим образом:

«x (есть) отец»: А¹(x) «x (есть) отец y»: А²(x, y)

ОО: люди ОО: упорядоченные

пары людей

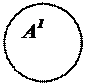Область истинности предиката [, выражаемого предикатором] Аⁿ(x₁, x₂ ,…,x_n)[,] обозначается на схеме символом Аⁿ без переменных (n=1,2,3,...). Здесь символы Аⁿ, x₁, x₂ ,…,x_n являются символами метаязыка; Аⁿ – метапеременная, пробегающая по n-местным предикатным константам языка-объекта, x₁, x₂ ,…,x_n – метапеременные, пробегающие по индивидным переменным символам языка-объекта; скобки, запятые, многоточие использованы автонимно.

Записанные в квадратных скобках выражения в дальнейшем мы будем опускать, то есть вместо полной записи «предикат, выражаемый предикатором Аⁿ(x₁, x₂ ,…,x_n) », мы будем использовать сокращенную запись «предикат Аⁿ(x₁,x₂ ,…,x_n )».

ПС.3.3. Элементарный коннектор в каждой интерпретации выражает n-местную истинностную функцию (n=1, 2), то есть функцию, ОО которой является { и, л } (при n=1) или двучленные кортежи предметов из { и, л } (при n=2), а ОЗ – { и, л }.

Область определения n-местной истинностной функции состоит из 2ⁿ элементов; поэтому истинностные функции задаются с помощью таблиц.

Коннектор (Øp) выражает истинностную функцию, задаваемую таблицей 2.3.

Таблица 2.3

p	(Ø p)
и	л
л	и

Дизъюнкция в современной логике выражает две истинностные функции: одна называется нестрогой (неисключающей) дизъюнкцией и выражается знаком Ú, а другая называется строгой (исключающей) дизъюнкцией и выражается знаком Ú (или знаком Ú с каким-нибудь другим дополнением).

Элементарные коннекторы (p Ú q) (дизъюнкция неисключающая), (p Ú q) (дизъюнкция исключающая), (p «q) (эквиваленция), (p ® q) (импликация) выражают истинностные функции, задаваемые таблицей (внешние скобки в записи ППФ в дальнейшем опускаются):

Таблица 2.4

p	q	p Ù q	p Ú q	p Ú q	p ® q	p «q
и	и	и	и	л	и	и
и	л	л	и	и	л	л
л	и	л	и	и	и	л
л	л	л	л	л	и	и

При переводе выражений естественного языка на ЯЛФРТ следует постоянно иметь в виду различие семантики предложений естественного языка и ЯЛФРТ, а именно: повествовательное предложение естественного языка обозначает положение дел (ситуацию) в некоторой предметной области, а предложение ЯЛФРТ обозначает один из двух абстрактных предметов: и или л. Поэтому семантика грамматических союзов «... и...», «... или...», «если..., то», «неверно, что...» в естественном языке не совпадает с семантикой коннекторов ЯЛФРТ, которые выражают связи лишь между истинностными значениями предложений, а не между обозначаемыми ими (в естественном языке) положениями дел. Например, такие предложения естественного языка, как (1) «Число 18 делится на 9 без остатка и число 27 делится на 9 без остатка», (2) «Число 18 делится на 9 без остатка, а число 12 не делится на 9 без остатка», (3) «Если число 18 делится на 9 без остатка, то число 12 не делится на 9 без остатка» будут записаны в ЯЛФРТ с помощью конъюнкции: (1) АÙВ, (2) АÙØ С, (3) АÙØС, где А интерпретируется как предложение «Число 18 делится на 9 без остатка»; В – как «Число 27 делится на 9 без остатка»; С – как «Число 12 делится на 9 без остатка». Предложения (1), (2), (3) естественного языка содержат разные грамматические союзы, поскольку предложением (1) утверждается одинаковость, сходство, подобие ситуаций, обозначаемых составляющими его простыми предложениями, а предложениями (2) и (3) утверждается противоположность этих ситуаций. При переводе этих предложений на ЯЛФРТ существенным оказывается то обстоятельство, что каждое из этих трех сложных предложений истинно если и только если истинны составляющие их предложения, что как раз и выражается логическим союзом конъюнкцией.

Таким образом, в естественном языке конъюнкция может быть представлена грамматическими союзами «... и...», «..., а...», «если..., то...» или знаками препинания («Дело под вечер. Зимой»). Отметим также, что бессмысленные с точки зрения семантики естественных языков предложения (например, «В огороде бузина, а в Киеве дядька») при переводе на ЯЛФРТ становятся осмысленными конъюнктивными предложениями.

Дизъюнкция (исключающая и неисключающая) представлена в естественном языке союзами «... или...», «или..., или...», «... и...» («Доктора наук и доценты могут участвовать в конкурсе на замещение должности заведующего кафедрой»), или знаками препинания. О какой дизъюнкции (строгой или нестрогой) идет речь в предложении естественного языка, выясняется из контекста.

Тот смысл, который выражается импликацией ЯЛФРТ, в традиционной логике называется «материальной импликацией» (Аристотель). Материальная импликация фиксирует лишь один из многочисленных смыслов союза «если..., то...» в естественном языке. Чаще всего «если..., то...» естественного языка выражает причинно-следственную связь или связь основание-следствие между положениями дел, обозначаемыми предложениями естественного языка; поэтому при переводе предложений естественного языка на ЯЛФРТ возникают «парадоксы материальной импликации».

I парадокс: Предложение «Если 2х2=4, то Наполеон – император», бессмысленное в естественном языке, является осмысленным в ЯЛФРТ и даже истинным (так как истинны оба члена импликативного предложения).

II парадокс: Предложение «Если 2х2=5, то Наполеон – император», бессмысленное в естественном языке, также является истинным в ЯЛФРТ (третья строка таблицы 2.4 для импликации).

III парадокс: Предложение «Если 2х2=5, то Наполеон – Герой России», бессмысленное в естественном языке, также является истинным в ЯЛФРТ (четвертая строка таблицы 2.4 для импликации).

Смысл союза «если..., то _***», фиксируемый материальной импликацией, лучше всего передается конструкцией «неверно, что (... и не _***)».

Конъюнкция, дизъюнкция (строгая и нестрогая) и эквиваленция являются симметричными логическими союзами, то есть истинностное значение сложного предложения, образованного с помощью этих союзов, не меняется при перемене мест составляющих предложений. Импликация не является симметричным коннектором; первый член импликации обычно называют антецедентом (от латинского antecedens – предшествующий), а второй – консеквентом (от латинского consequius – последующий). Антецедент импликации называют также достаточным условием (для консеквента), а консеквент – необxодимым условием (для антецедента). Предложение ЯЛФРТ А®В может быть представлено одной из конструкций естественного языка: (1) «если А, то В»; (2) «В, если А»; (3) «А достаточно для того, чтобы В»; (4) «В необходимо для того, чтобы А». Слово «только», поставленное перед словом «если» в предложении естественного языка, равнозначно по смыслу перемене мест членов импликации. Например, предложение «Если Алик за рулем, то мы едем с превышением скорости» запишется в ЯЛФРТ формулой «А®В», где А представляет предложение «Алик за рулем», а В – «Мы едем с превышением скорости», в то время как предложение «Только если Алик за рулем, то мы едем с превышением скорости» запишется в ЯЛФРТ формулой «В®А».

Кроме указанных способов выражения, материальная импликация может быть представлена в естественном языке словами «следовательно», «значит», «поэтому», «потому что», «так как».

Наличие у грамматического союза естественного языка «если..., то...» смысла, выражаемого материальной импликацией, можно проиллюстрировать следующим примером.

Пример 2.8. Предложение «Если число а делится без остатка на 4, то оно делится без остатка на 2» является истинным в арифметике натуральных чисел, то есть оно должно быть истинным для любого натурального числа.

1 случай. Пусть мы взяли число а =12, тогда предложение «Число 12 делится без остатка на 4» будет истинно и предложение «Число 12 делится без остатка на 2» тоже истинно; это соответствует первой строке в таблице 2.4. для импликации.

2 случай. Пусть мы взяли число а =10. Тогда антецедент импликации будет ложным, консеквент истинным, а все предложение истинным, что соответствует третьей строке в таблице 2.4. для импликации.

3 случай. Пусть мы взяли число а =11. Тогда и антецедент, и консеквент импликации будут ложными, а все предложение –

истинным, что соответствует четвертой строке в таблице 2.4 для импликации.

Какое бы число мы ни взяли, мы никогда не получим случай, когда антецедент импликации будет истинным, а консеквент ложным. Значит смысл данного предложения можно передать словами: «Не может быть, что (неверно, что) число делится на 4 без остатка ине делится на 2 без остатка».

Эквиваленция представляется в естественном языке словами «... если и только если...», «... тогда и только тогда, когда...», «...необходимо и достаточно для того, чтобы...» и т.д.

Составными коннекторами будем называть составные коннекторные ППФ, содержащие, кроме символов коннекторов, только пропозициональные переменные.

Истинностные функции, выражаемые составными коннекторами, представляются таблицами, в которых сопоставление значений и и л наборам значений переменных осуществляется последовательно, по строению ППФ.

Пример 2.9. Неэлементарный составной коннектор pÙq®r (скобки опущены в соответствии с соглашением о скобках) выражает истинностную функцию, задаваемую следующей таблицей.

p	q	r	p Ù q	p Ù q ® r
и	и	и	и	и
и	и	л	и	л
и	л	и	л	и
л	и	и	л	и
и	л	л	л	и
л	и	л	л	и
л	л	и	л	и
л	л	л	л	и	.

Истинностные функции могут выражаться не только правильно построенными формулами языка-объекта, но и выражениями метаязыка. Так, например, всякая ППФ вида AÙВ®C (скобки опущены в соответствии с соглашением о скобках) выражает ту же самую истинностную функцию, что и ППФ pÙq®r:

А	В	С	АÙВ	АÙВ®С
и	и	и	и	и
и	и	л	и	л
и	л	и	л	и
л	и	и	л	и
и	л	л	л	и
л	и	л	л	и
л	л	и	л	и
л	л	л	л	и	.

В нижеследующих семантических правилах для кванторных выражений ПС.3.4." и ПС.3.5.$ символ А¹ – метапеременная по одноместным предикатным константам, х – метапеременная по индивидным переменным, В(х) – метапеременная по ППФ, содержащим индивидную переменную х в качестве единственной свободной переменной, символы кванторов и скобки использованы автонимно. Согласно ФИО ППФ В(х) является одноместным предикатором (элементарным или составным).

ПС.3.4.". Предложение "_А1_(x)В(x)истинно, если и только если предикат [, выражаемый предикатором] В (x) ставит в соответствие значение и всем тем предметам из области своего определения, которым ставит в соответствие значение и предикат [, выражаемый предикатором] А¹(x).

В дальнейшем выражения в квадратных скобках будут опускаться.

ПС.3.5.$. Предложение $_А1_(x)В (x)истинно, если и только если предикат В(x) ставит в соответствие значение и хотя бы одному предмету из области своего определения, которому ставит в соответствие значение и предикат А¹(x).

В классической логике кванторные выражения считаются осмысленными при выполнении следующих условий:

(1) предикаты А¹(x) и В(x) имеют общую область определения (то есть общую предметную область);

(2) область истинности предикатов А¹(x) и В(x) не пуста и не совпадает с их ПрО.

При выполнении этих условий значение истинности кванторного предложения определяется отношением областей истинности предикатов, выражаемых ППФ А¹(x) и В(x), что демонстрируется схемой 2.5.