Схема 2.6

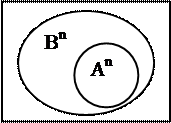
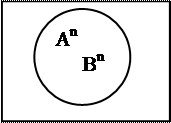
Аⁿ = Вⁿ Аⁿ Ì Вⁿ

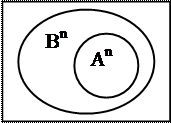
Аⁿ Í Вⁿ

или

.

С помощью экстенсиональной абстракции в стандартной теоретико-множественной семантике n-местная операция отождествляется с (n+1)–местным предикатом, а (n+1)–местный предикат отождествляется с множеством (классом) истинности этого предиката.

Пример 2.13. Двухместная операция «х+у» (символически +²(х, у); х, у пробегают по действительным числам) отождествляется с трехместным предикатом «х+у=z» (символически А³(х,у,z); х, у, z пробегают по действительным числам), а предикат А³(х,у,z) отождествляется с множеством истинности данного предиката. Таким образом, при экстенсиональной абстракции не различаются такие абстрактные объекты, как l _х,у+²(х,у) (двуместная операция сложение) и { áх,у,zñ ½ х+у=z }.

Экстенсиональная абстракция лежит в основе теории множеств, а также в основе теоретико-множественнойматематики и теоретико-множественной семантики. В стандартной теоретико-множественной семантике ЯЛФРТ универсум рассуждения содержит, кроме исходных предметов, также всевозможные множества предметов и n-членных кортежей этих предметов (n=2,3,…). При стандартной теоретико-множественной семантике ЯЛФРТ можно вообще обойтись без операторных функциональных символов: индивидные константы рассматриваются как имена предметов из универсума рассуждения, индивидные переменные принимают значения в (пробегают по) универсуме(-у) рассуждения, предикатные n–местные константы рассматриваются как имена множеств n–членных кортежей предметов из универсума рассуждения, а предикатные n–местные переменные пробегают по области множеств n–членных кортежей предметов из универсума рассуждения. Функторные переменные в стандартной теоретико-множественной семантике ЯЛФРТ считаются пробегающими по всем функциям, определенным на области интерпретации, а не только по тем функциям, которые могут быть выражены с помощью выразительных средств данного ЯЛФРТ; в случае счетно-бесконечной области интерпретации в стандартной теоретико-множественной семантике множество функций, определенных на этой области интерпретации, становится несчетным, что является источником больших затруднений в основаниях теоретико-множественной математики.