Даны вершины треугольника АВС. Найти:
1) общее уравнение стороны АВ;
2) длину стороны ВС;
3) уравнение высоты, опущенной из вершины А;
4) систему неравенств, определяющих треугольник АВС.
| 1. | А (2; -1), | В (-2; -2), | С (3; 4). |
| 2. | А (12; 0), | В (18; 8), | С (0; 5). |
| 3. | А (-2; -6), | В (-6; -3), | С (10; -1). |
| 4. | А (8; 2), | В (14; 10), | С (-4; 7). |
| 5. | А (2; -4), | В (-2; -1), | С (14; 1). |
| 6. | А (2; -1), | В (8; 7), | С (-10; 4). |
| 7. | А (5; -3), | В (1; 0), | С (17; 2). |
| 8. | А (14; -6), | В (20; 2), | С (2; -1). |
| 9. | А (3; 4), | В (-1; 7), | С (15; 9). |
| 10. | А (1; -2), | В (7; 6), | С (-11; 3). |
| 11. | А (2; -1), | В (-2; -2), | С (3; 4). |
| 12. | А (12; 0), | В (18; 8), | С (0; 5). |
| 13. | А (-2; -6), | В (-6; -3), | С (10; -1). |
| 14. | А (8; 2), | В (14; 10), | С (-4; 7). |
| 15. | А (2; -4), | В (-2; -1), | С (14; 1). |
| 16. | А (2; -1), | В (8; 7), | С (-10; 4). |
| 17. | А (5; -3), | В (1; 0), | С (17; 2). |
| 18. | А (14; -6), | В (20; 2), | С (2; -1). |
| 19. | А (3; 4), | В (-1; 7), | С (15; 9). |
| 20. | А (1; -2), | В (7; 6), | С (-11; 3). |
| 21. | А (2; -1), | В (-2; -2), | С (3; 4). |
| 22. | А (12; 0), | В (18; 8), | С (0; 5). |
| 23. | А (-2; -6), | В (-6; -3), | С (10; -1). |
| 24. | А (8; 2), | В (14; 10), | С (-4; 7). |
| 25. | А (2; -4), | В (-2; -1), | С (14; 1). |
| 26. | А (2; -1), | В (8; 7), | С (-10; 4). |
| 27. | А (5; -3), | В (1; 0), | С (17; 2). |
| 28. | А (14; -6), | В (20; 2), | С (2; -1). |
| 29. | А (3; 4), | В (-1; 7), | С (15; 9). |
| 30. | А (1; -2), | В (7; 6), | С (-11; 3). |
Задание №6
Определить, какие линии задаются уравнениями. Найти их геометрические характеристики. Построить линии.
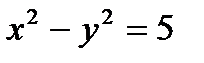
| 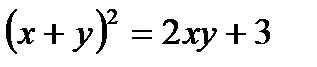
| 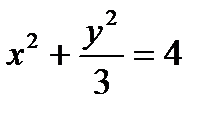
| |||
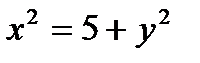
| 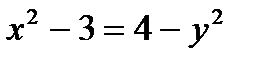
| 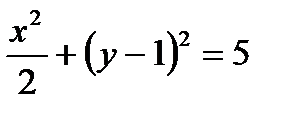
| |||
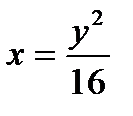
| 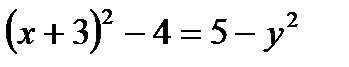
| 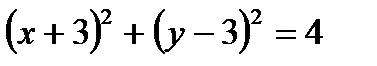
| |||
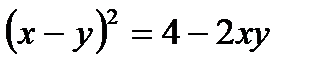
| 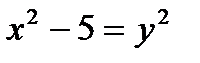
| 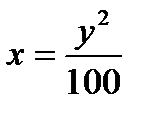
| |||
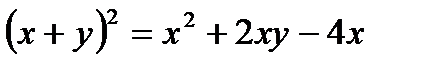
| 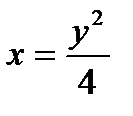
| 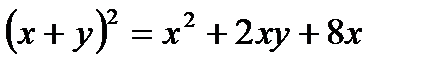
| |||
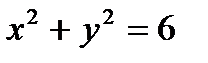
| 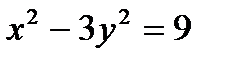
| 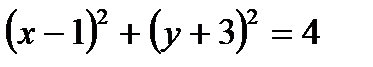
| |||
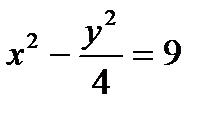
| 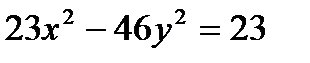
| 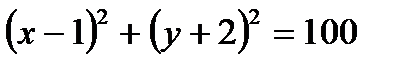
| |||
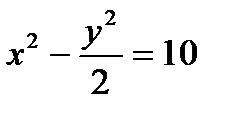
| 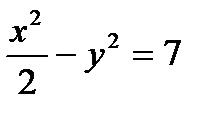
| 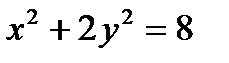
| |||
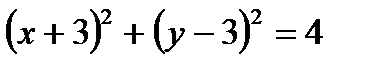
| 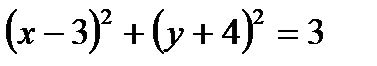
| 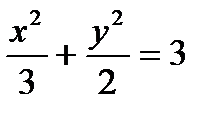
| |||
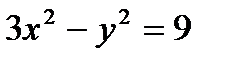
| 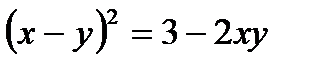
| 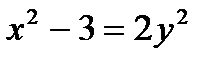
|
Задание №7
Найти расстояние от точки М(1,2, 3) до плоскости, проходящей через три точки А, В, С.
| 1. | А1(4, 2, 5), | А2(0, 7, 2), | А3(0, 2, 7), |
| 2. | А1(4, 4, 10), | А2(4, 10, 2), | А3(2, 8, 4), |
| 3. | А1(4, 6, 5), | А2(6, 9, 4), | А3(2, 10, 10), |
| 4. | А1(3, 5, 4), | А2(8, 7, 4), | А3(5, 10, 4), |
| 5. | А1(10, 6, 6), | А2(-2, 8, 2), | А3(6, 8, 9), |
| 6. | А1(1, 8, 2), | А2(5, 2, 6), | А3(5, 7, 4), |
| 7. | А1(6, 6, 5), | А2(4, 9, 5), | А3(4, 6, 11), |
| 8. | А1(7, 2, 2), | А2(5, 7, 7), | А3(5, 3, 1), |
| 9. | А1(8, 6, 4), | А2(10, 5, 5), | А3(5, 6, 8), |
| 10. | А1(7, 7, 3), | А2(6, 5, 8), | А3(3, 5, 8), |
| 11. | А1(4, 2, 5), | А2(0, 7, 2), | А3(0, 2, 7), |
| 12. | А1(4, 4, 10), | А2(4, 10, 2), | А3(2, 8, 4), |
| 13. | А1(4, 6, 5), | А2(6, 9, 4), | А3(2, 10, 10), |
| 14. | А1(3, 5, 4), | А2(8, 7, 4), | А3(5, 10, 4), |
| 15. | А1(10, 6, 6), | А2(-2, 8, 2), | А3(6, 8, 9), |
| 16. | А1(1, 8, 2), | А2(5, 2, 6), | А3(5, 7, 4), |
| 17. | А1(6, 6, 5), | А2(4, 9, 5), | А3(4, 6, 11), |
| 18. | А1(7, 2, 2), | А2(5, 7, 7), | А3(5, 3, 1), |
| 19. | А1(8, 6, 4), | А2(10, 5, 5), | А3(5, 6, 8), |
| 20. | А1(7, 7, 3), | А2(6, 5, 8), | А3(3, 5, 8), |
| 21. | А1(4, 2, 5), | А2(0, 7, 2), | А3(0, 2, 7), |
| 22. | А1(4, 4, 10), | А2(4, 10, 2), | А3(2, 8, 4), |
| 23. | А1(4, 6, 5), | А2(6, 9, 4), | А3(2, 10, 10), |
| 24. | А1(3, 5, 4), | А2(8, 7, 4), | А3(5, 10, 4), |
| 25. | А1(10, 6, 6), | А2(-2, 8, 2), | А3(6, 8, 9), |
| 26. | А1(1, 8, 2), | А2(5, 2, 6), | А3(5, 7, 4), |
| 27. | А1(6, 6, 5), | А2(4, 9, 5), | А3(4, 6, 11), |
| 28. | А1(7, 2, 2), | А2(5, 7, 7), | А3(5, 3, 1), |
| 29. | А1(8, 6, 4), | А2(10, 5, 5), | А3(5, 6, 8), |
| 30. | А1(7, 7, 3), | А2(6, 5, 8), | А3(3, 5, 8), |
 2015-04-12
2015-04-12 245
245








