x, y∈ ε n, А∈L(ε n).
[e]= 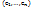 — ОНБ
— ОНБ
[e]: A↔Aе – матр. А в [e]ю
1° Операт. А явл. самосопр., т. и т.т., когда ∀ ij – 1, …, n, 
1) Необходимость: очевидна
2) Достаточность:
Пусть ∀x, y∈ ε n, 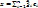 ,
, 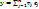
 ;
; 
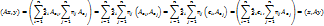
2° Оператор А явл. Самосопряж. т. т т.т., когда матр. Ае в произв. ОНБ явл. симметричной.
Док-во:

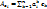 ,
, 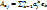
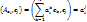
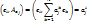
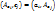 , т.е..
, т.е.. 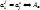 – симметричн. (т.е..
– симметричн. (т.е.. 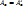 ).
).
3° Теорема
Все корни характерист-го многочл. симметричной матрицы действ. числа (без док-ва).
4° Всякий самосопряж. оператор имеет собств. вектор.
Док-во:
Пусть А – самосопряж., [e] – ОНБ; A↔ Aе симметричная. Все собств. знач. А – действ. корни мн-на 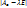 по св-ву 3° мн-н имеет действ. корень, это собств. знач. А, → ∃ собств. вектор.
по св-ву 3° мн-н имеет действ. корень, это собств. знач. А, → ∃ собств. вектор.
5° Собств. вектора относящ. к различным собств. знач. самосопряж. оператора ортогональны.
Док-во:
∀x, y: (Ax, y)=(x, Ay)
λ1, λ2∈ℝ, λ1≠λ2, ∃е1, е2 — ненулевые.
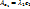 ;
; 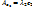 .
.
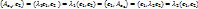
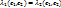 , т.к.. λ1≠λ2, то
, т.к.. λ1≠λ2, то 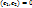 , то есть
, то есть 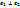 .
.
 2015-04-12
2015-04-12 315
315








