Спектральная теорема самосопряженного оператора

Теорема: линейный оператор А евклидова пространства E_n является самосопряженный тогда и только тогда, когда в E_n ∃ ортонормированный базис, состоящий из собственных векторов вектора A.

Док-во:

1) Пусть в [e] – ортонормированный базис пространства E_n A ⇔A_e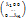

Когда = A_e=>A самосопряженный

2) Пусть А- самосопряженный оператор E_n. Т.к. А самосопряженный, то ∃ — собственное значение А

и соответственно собственный вектора e₁≠0, Ae₁= λ₁e_1.Считаешь, что lle_xll=1, т.е. при n=1 теорема верна

Док-во:

1) Основ. n=1

2) Допустим, что теорема справедлива ∀E – евклидова пространства, dim E=n-1

3) Пусть dim E= n, т.е..Е=E_n

А самосопряженный оператор E_n

В E_n ∃e₁ – собственный вектор А

Аe₁= λ₁e₁; lle₁ll=1

В E_n∃ базис e₁, f₂…f_n – базис E_{n —} ОНБ