На практике для выпуска планового объема валовой продукции Х требуется использовать следующие ограниченные (дефицитные) ресурсы производства:
а) производственные фонды (основные, оборотные, заработная плата);
б) природные ресурсы (воды, ископаемые, леса);
в) трудовые ресурсы;
г) продукция других внешних систем (импорт);
д) другие виды ресурсов.
Включение дефицитных ресурсов в модель осуществляется следующим образом.
Пусть имеется m дефицитных ресурсов R 1, R 2,¼, Rm и их потребление отраслями за отчетный период известно (табл. 2).
Обозначим через rij – количество i -ресурса, потребленного j -отраслью; 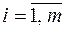 ;
; 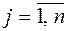 :
:
R 1 = r 11 + r 12 + ¼ + r 1 n,
R 2 = r 21 + r 22 + ¼ + r 2 n , (10)
¼
Rm = rm 1 + rm 2 + ¼ + rmn.
Таблица 2. Схема межотраслевого баланса с учетом дефицитных ресурсов
| Производящие отрасли | Потребляющие отрасли | Конечная продукция, Y | Валовая продукция, Х | |||
| ¼ | n | |||||
| x 11 | x 12 | ¼ | x 1 n | Y 1 | X 1 | |
| x 21 | x 22 | ¼ | x 2 n | Y 2 | X 2 | |
| ¼ | ¼ | ¼ | ¼ | ¼ | ¼ | |
| n | xn 1 | xn 2 | ¼ | xnn | Yn | Xn |
| Ресурсы | ||||||
| r 11 | r 12 | ¼ | r 1 n | |||
| r 21 | r 22 | ¼ | r 2 n | |||
| ¼ | ¼ | ¼ | ¼ | |||
| m | rm 1 | rm 2 | ¼ | rmn |
Количество израсходованных ресурсов и объем произведенной валовой продукции связывают коэффициенты прямых затрат ресурсов, которые можно представить в виде матрицы:
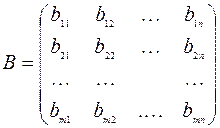 , (11)
, (11)
где 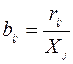 ;
; 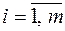 ;
; 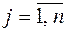 .
.
Величины bij в балансовых моделях не зависят от объема потребления ресурсов в отрасли и являются стабильной величиной во времени.
Коэффициенты прямых затрат ресурсов bij обозначают объем i -ре-
сурса, необходимого для производства единицы продукции j -отрасли.
Пусть на планируемый период известны выделенные объемы каждого ресурса Rп. Их количество должно обеспечивать выпуск валовой продукции Хп в требуемом объеме. Зная коэффициенты прямых затрат ресурсов bij, можно рассчитать требующийся объем ресурсов каждого вида Riтр, необходимых для выпуска валовой продукции Хп в требуемом объеме:
R 1 тр = b 11 X 1 п + b 12 X 2 п + ¼ + b 1 n Xn п;
R2 тр = b 21 X 1 п + b 22 X 2 п + ¼ + b 2 n Xn п; (12)
¼
Rт тр = bт 1 Xт п + bт 2 X 2 п +¼+ bтn Xт п.
Систему уравнений (12) можно записать в матричной форме:
Rтр = ВX, (13)
где 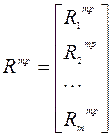 – вектор-столбец требующихся ресурсов.
– вектор-столбец требующихся ресурсов.
Для обеспечения планируемого выпуска валовой продукции Хп необходимо выполнение следующего условия:
Rтр £ Rп. (14)
Система (12) позволяет найти общие потребности в ресурсах при заданном объеме валовой продукции.
 2015-04-17
2015-04-17 316
316








