Математические модели систем

Математическая модель системы складывается из математических моделей звеньев. На рис. 17.1 модели звеньев представлены в виде передаточных функций.

Модель каждого звена представляет собой связь выходного сигнала, соответствующего назначению элемента, и входного сигнала равного выходному сигналу предшествующего элемента системы.

Точно такой же подход применяется и при получении моделей систем в виде их передаточных функций.

Выходным сигналом системы является регулируемая величина, являющаяся целью работы системы. Для разных по назначению систем она должна либо оставаться постоянной (системы стабилизации), либо меняться системой по заданному закону (программные системы), либо по случайно меняющемуся заданию (следящие системы).

Из этого следует, что передаточная функция системы должна отражать связь регулируемой величины и задающего воздействия.

По определению такая передаточная функция Ф(p) есть отношение изображений по Лапласу регулируемой величины Y(p) к изображении по Лапласу задающего воздействия G(p) при нулевых начальных условиях т.е.

Ф(p)= 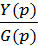. (17.1)

Другой передаточной функцией системы, отражающей влияние на регулируемую величину возмущающего воздействия F, служит передаточная функция системы по возмущению

Ф_f(p)= 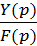. (17.2)

При необходимости исследовать точность работы системы при отработки ей задающего воздействия G используется

передаточная функция системы по ошибке X регулирования

Ф_x(p)= 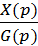(17.3)

Из рис.17.1 структурная схема системы включает типы соединений звеньев, встречающихся в системах.

Так, звенья 1 и 2 (передаточные функции W₁ (p), W₂(p)) соединены последовательно, 6 и 7 параллельно, а звено 3 охвачено обратной связью звеном 4. В этом случае говорят о местной обратной связи, которая, в отличие от главной обратной связи, может быть не только отрицательной, но и положительной.

У последовательных звеньев выходной сигнал предыдущего звена является входным для последующего.

Модель такого соединения звеньев, дающая связь их выходного сигнала (в данном случае y₁) с входным сигналом (y₂) равна произведению передаточных функций звеньев

W_1-2 (p) = 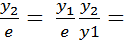W₁(p) W₂(p).

В общем случае, при соединенных последовательно n звеньях их модель - эквивалентная передаточная функция W_э (p) будет равна

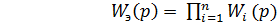. (17.4)

При параллельном соединении все звенья имеют один общий входной сигнал, а их выходные сигналы складываются.

В этом случае модель такого соединения можно получить, записав последовательно

y₆=Y·W₆(p), y₇=Y·W₇(p),

y₈= y₆+y₇= Y·W₆(p)+ Y·W₇(p)= (W₆(p)+ W₇(p))·Y.

Таким образом эквивалентная передаточная функция параллельного соединения звеньев равна

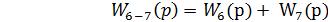
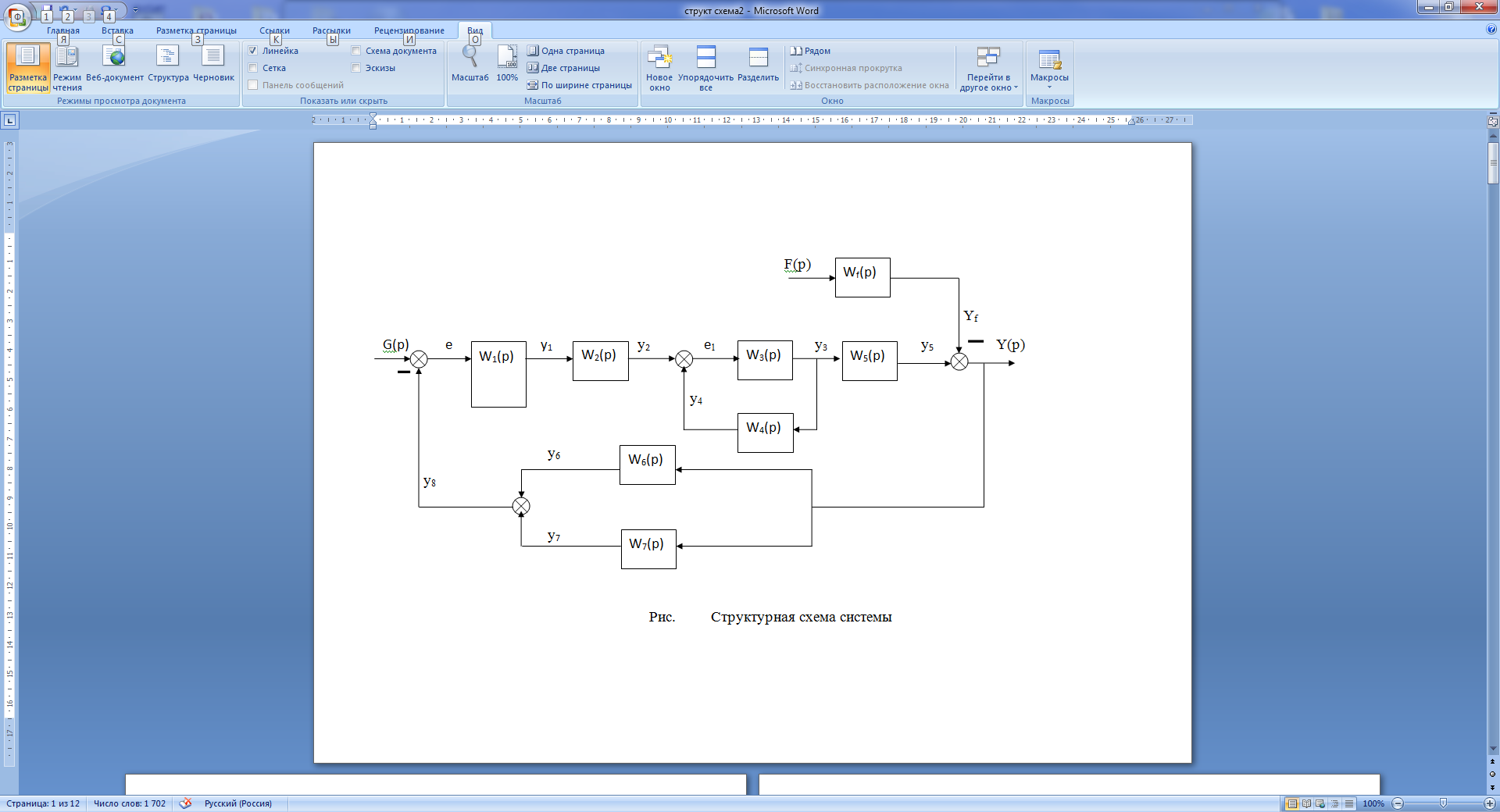
Рис.17.1. Структурная схема системы

или в общем случае для n параллельных звеньев можно записать

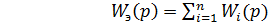. (17.5)

Для соединений звеньев с обратной связью запишем

e₁= y₂+y₄ (17.6)

Знак + (положительная обратная связь), так как сигналы складываются, а в случае вычитания y₄ (отрицательная обратная связь) ставится знак.

Продолжим

y₃ = e₁ W₃(p), (17.7)

y₄ = y₃ W₄(p). (17.8)

Зависимость y₃ от y₂ получим, исключая промежуточные переменные e₁ и y₄:

y₃ = 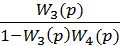y₂, (17.9)

а эквивалентная передаточная функция будет равна

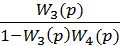. (17.10)

В случае отрицательной обратной связи выражение для эквивалентной передаточной функции (17.10) имело бы вид

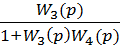. (17.11)

Вернемся к получению передаточной функции системы
Ф(p)= 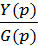. (17.12)

Существующий метод преобразования структурных схем заключается в поэтапной замене соединений звеньев их эквивалентами.

В этом случае, применяя данный метод, получим

Рис. 17.2 Последовательность структурных преобразований исходной структурной схемы системы.

Получив передаточную функцию Ф(p), имеем возможность решать задачи анализа и синтеза системы: изучать выполнение системой задачи поддержания соответствия регулируемой величины задающему воздействию с заданной точностью и в случае неудовлетворительного исполнения вносить необходимые изменения в ее структуру.

Как было отмечено, наряду с рассмотренной передаточной функцией системы «по каналу» G(p) - Y(p), для исследования поведения (работы, функционирования) системы при возмущающем воздействии F(p) (в общем случае при нескольких внешних воздействиях) необходимо получить и соответствующую передаточную функцию системы (передаточные функции) по возмущающему воздействию Ф_F(p) = 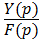или, как говорят, «по каналу возмущающего воздействия» F(p) - Y(p).

Методы суперпозиции и гомогенности, применимые к линейным системам, позволяют изучать систему и ее поведение раздельно по задающему и возмущающему воздействиям.

Так, для получения передаточной функции системы по возмущающему воздействию полагают G(t) = 0.

Воспользуемся первыми результатами предыдущих преобразований

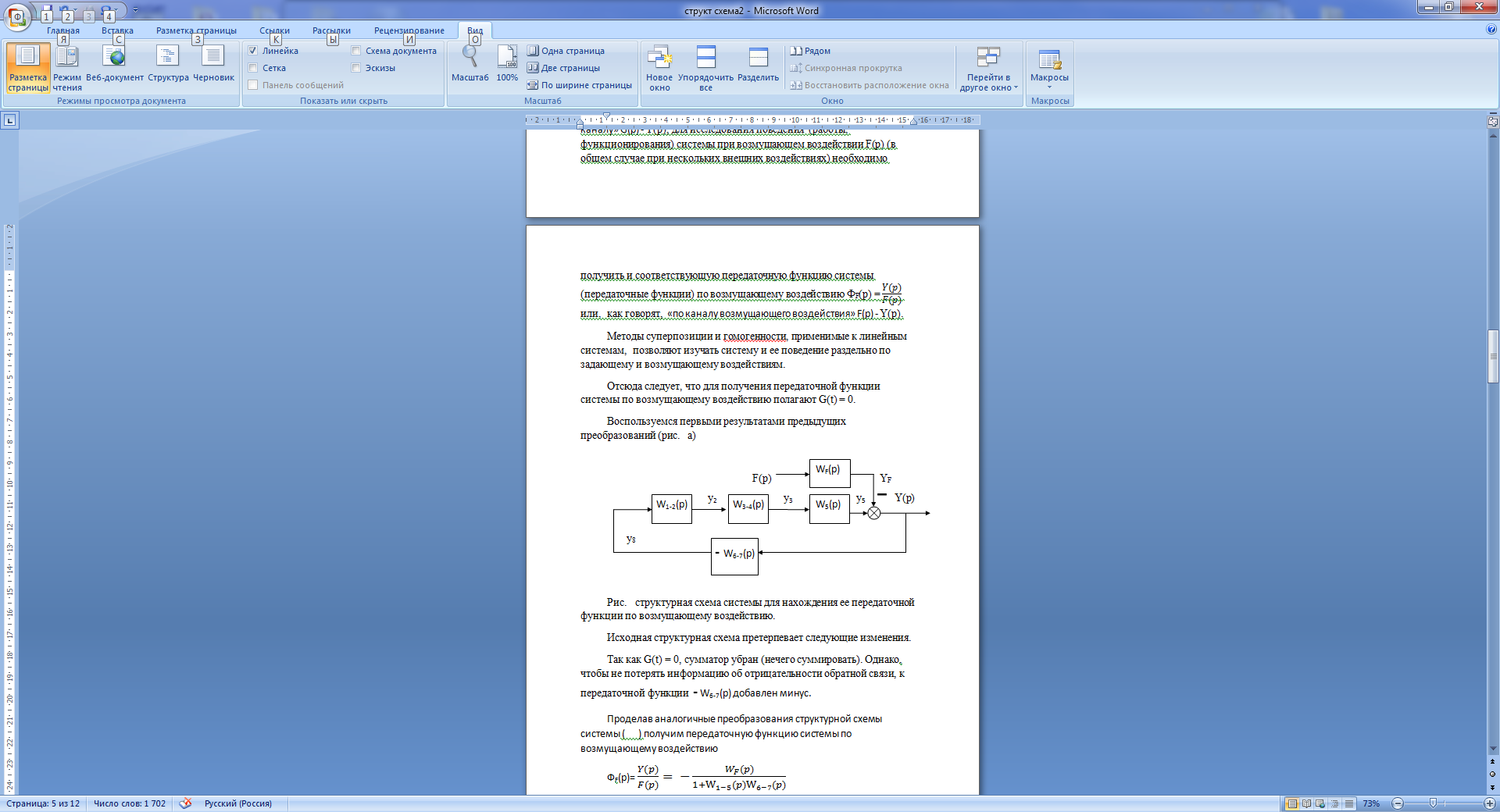
Рис. 17.3. Структурная схема системы для нахождения ее передаточной функции по возмущающему воздействию

Исходная структурная схема, с учетом проделанных ранее преобразований, претерпевает следующие изменения (рис.17.3).

Так как G(t) = 0, сумматор убран (нечего суммировать). Однако, чтобы не потерять информацию об отрицательности обратной связи, к передаточной функции - W_6-7(p) добавлен минус.

Проделав аналогичные преобразования структурной схемы системы (17.3) получим передаточную функцию системы по возмущающему воздействию

Ф_F(p)= 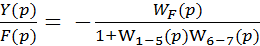. (17.13)

Для исследований поведения системы при возмущающем воздействии определяется результат такого воздействия в изображении по Лапласу Y(p).

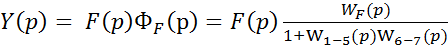. (17.14)

Далее, пользуясь обратным преобразованием Лапласа, находится Y(t) = L^-1[Y(p)], строится график Y(t) и по нему выносятся суждения о работе системы при действии на нее возмущения.

При исследовании точности работы систем может потребоваться информация об ошибке регулирования. В этом случае находится передаточная функция Ф_х(p)= 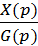и x(p)= 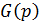Ф_х(p), далее
X(t) = L^-1[X(p)].

В процессе исследования (моделирования) работы системы может возникнуть потребность получить сведения о поведении какой–либо выходной величины какого-либо элемента системы Х_выхЭ (t) при действии задающего или возмущающего воздействий.

Для ее решения необходимо находить соответственно либо передаточную функцию 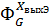(p) = 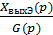, либо передаточную функцию
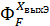(p) = .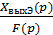

Замечание.

Исходная модель любого элемента системы – дифференциальное уравнение, полученное при рассмотрении происходящих в нем процессов. Имея систему уравнений элементов системы, можно получить уравнение системы, исключая промежуточные переменные. Однако такая задача достаточно трудоемка, поскольку пришлось бы иметь дело с производными, в ряде случаев не малых порядков. При использовании преобразования Лапласа приходится иметь дело лишь с арифметическими операциями, что намного проще.

При желании иметь уравнение системы в виде дифференциального уравнения достаточно в соответствующей передаточной функции системы произвести формальную замену p на 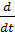, т.е. операцию, обратную операции получения передаточной функции из дифференциального уравнения.

В дальнейшее изложении встретятся различные способы, помогающие упростить математические выкладки.

По высказыванию философа Маха «математика позволяет экономить мысль и время». К этому сегодня можно было бы добавить «и затрачиваемые на решение задач средства».

Для того чтобы реализовать возможности упрощать решения ряда задач в дальнейшем, рассмотрим структурную схему системы.

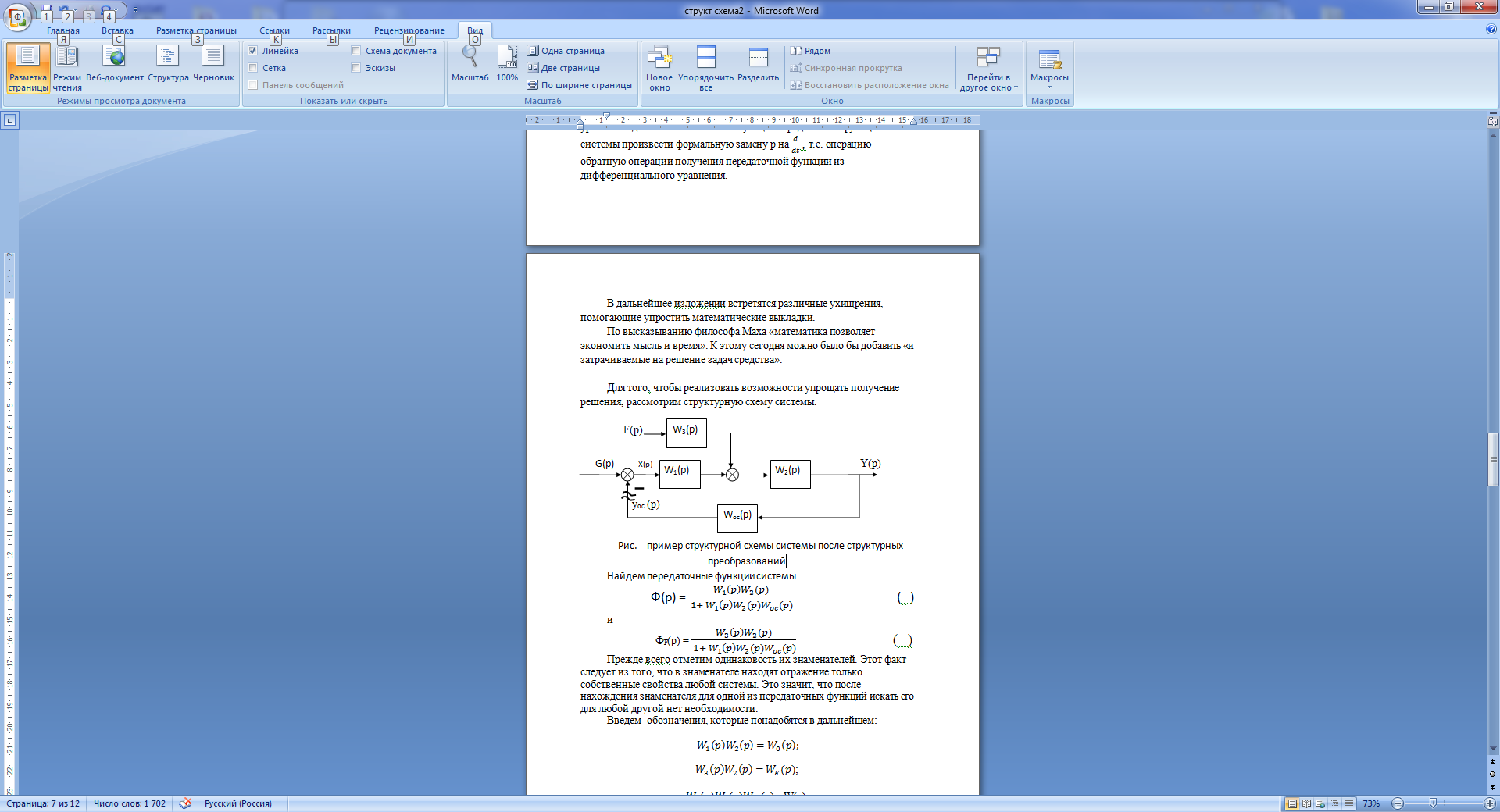
Рис.17.4. Пример структурной схемы системы после структурных преобразований

Найдем передаточные функции системы

Ф(p) = 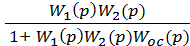(17.15)

и

Ф_F(p) = 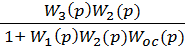. (17.16)

Прежде всего, отметим одинаковость их знаменателей. Этот факт следует из того, что в знаменателе находят отражение только собственные свойства любой системы. Это значит, что после нахождения знаменателя для одной из передаточных функций искать его для любой другой нет необходимости.

Введем обозначения, которые понадобятся в дальнейшем:

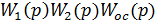= W(p). (17.19)

Условно разомкнем систему: символ на схеме, обратная связь прервана.

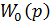- передаточная функция носит название передаточной функции разомкнутой системы по прямому каналу задающего воздействия.

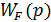- передаточная функция носит название передаточной функции разомкнутой системы по возмущающему воздействию.

W(p) – передаточная функция носит название передаточной функции разомкнутой системы и по определению представляет собой отношение 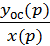= W(p).

Рассмотрим случай, когда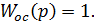

Будем иметь

Ф(p) = 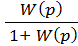. (17.20)

Между Ф(p) и 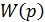существует взаимно-однозначное соответствие, т.е., например, есл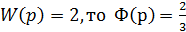и и,
если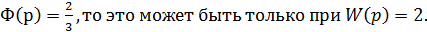

Это значит, что вся информация о свойствах системы, содержащаяся в 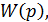отражается в Ф(p) и наоборот.

Отсюда, зная такую связь, появляется возможность оперировать с более простым выражением 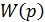при анализе и синтезе систем, чем с Ф(p), что в дальнейшем и будет использовано.