2015-04-17
801
Задание. Для рамы (рис. 4) с размерами и нагрузкой, полученными по табл. 5, требуется:
1. Определить степень статической неопределимости.
2. Выбрать основную систему метода сил и составить систему канонических уравнений в общем виде. Расчет следует выполнить с учетом возможных упрощений, сводящихся к наиболее «выгодной» основной системе.
3. Построить эпюры изгибающих моментов
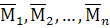
от действия на основную систему сил, соответственно равных
Х1=1, Х2=1, …, Хn=1.
4. Построить грузовую эпюру МР от действия на основную систему заданных внешних сил и эпюру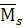 
(суммарную единичных эпюр изгибающих моментов).
5. Проверить правильность вычисленных перемещений.
6. Решить систему уравнений и проверить правильность ее решений. Нельзя при этом ограничиваться проверкой одного уравнения, найденные значения неизвестных нужно подставить во все уравнения и убедиться, что все они удовлетворяются.
7. Построить «исправленные» эпюры изгибающих моментов. Для этого ординаты эпюр от единичных воздействий
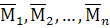
умножить соответственно на численные значения найденных неизвестных
Х1, Х2, …, Хn с учетом их знаков, т.е. построить эпюры
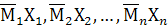
8. Построить действительную (окончательную) эпюру М относительно заданной рамы путем сложения «исправленных» эпюр с эпюрой МР.
9. Проверить правильность построения эпюры М:
а) статическая проверка;
б) деформационная проверка.
10. Построить эпюры поперечных Q и продольных N сил относительно заданной рамы.
11. Проверить правильность эпюр Q и N. Для этого необходимо провести сечение и отделить от рамы какую-нибудь часть. В местах рассечения приложить продольные, поперечные силы и изгибающие моменты, определенные с помощью эпюр М, Q и N. К отсеченной части рамы следует приложить также и заданные внешние силы. Если эпюры построены правильно, то будут удовлетворены условия равновесия отсеченной части рамы:
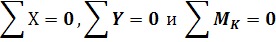
Таблица 5.
| 1 я цифра шифра | L1 м | q2 кН/м | 2 я цифра шифра | q1 кН/м | P2 кН | h2 м | 3 я цифра шифра | L2 м | P1 кН | h1 м |
| 3,8 | 6,2 | 8,0 | 3,2 | 4,5 | ||||||
| 3,6 | 6,4 | 10,6 | 3,2 | 3,0 | 4,7 | |||||
| 3,4 | 6,6 | 10,8 | 3,4 | 3,6 | 4,0 | |||||
| 4,4 | 6,8 | 3,6 | 6,0 | 3,5 | ||||||
| 4,6 | 8,0 | 12,6 | 3,8 | 5,6 | 3,7 | |||||
| 4,0 | 7,2 | 12,8 | 4,0 | 5,8 | 3,3 | |||||
| 4,8 | 7,4 | 4,2 | 4,5 | 5,0 | ||||||
| 5,0 | 7,6 | 14,6 | 5,0 | 4,4 | 4,2 | 5,2 | ||||
| 5,2 | 7,8 | 14,8 | 5,8 | 4,6 | 6,2 | 5,4 | ||||
| 5,4 | 9,0 | 4,0 | 6,0 | 4,8 | 6,4 | 5,6 |
Методические указания
Выбранная основная система должна быть обязательно геометрически неизменяемой. Для выбора основной системы следует сравнить между собой ряд вариантов и обосновать целесообразность принятой основной системы.
При определении коэффициентов и свободных членов канонических уравнений следует помнить, что жесткости стоек и ригелей не равны между собой. Проверка правильности определения величин коэффициентов и свободных членов выполняется подсчетом интегралов Мора.
Эпюра Q строится с помощью эпюры М. На участке, где эпюра М прямолинейна, значение Q определяется как тангенс угла наклона эпюры М. На участке, где эпюра М криволинейна, построение эпюры Q производится с помощью формулы
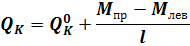
Эпюра N строится с помощью эпюры Q путем вырезания узлов, начиная с узла, в котором количество неизвестных продольных сил не превышает двух. При вырезании каждого узла необходимо учитывать, что положительная поперечная сила вращает узел по часовой стрелке, а отрицательная – против.
