2015-04-17
227
В пространстве переменных (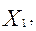
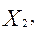
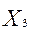) каждое из ограничений вида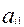 
+ 
+ 
= 
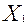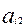
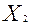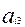
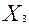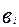по трудоемкости или металлоемкости определяет плоскость 
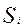, проходящую через точки:
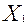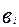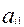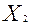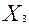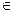
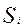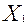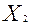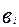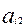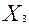( = / , = 0, = 0)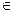 
,
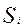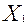( = 0, = / , = 0) ,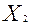
( = 0, = 0, = / ) ,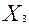
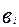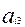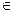
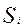i = 1, 2.
Пример изображения этих плоскостей приведен на рис. 1.
Точки, лежащие на линии пересечения плоскосте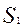й 
и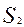 
, удовлетворяют ограничениям по трудоемкости и металлоемкости одновременно. При этом линия пересечения существует в силу принятого предположения об отсутствии взаимной зависимости ограничений.
Наконец, условия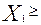 
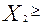0, 
0,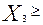 
0 определяют отрезок линии пересечения плоскосте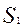й и 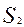, лежащий между координатными плоскостями. Такой отрезок тоже существует в силу сбалансированности ограничений. Точки отрезка (и только они) удовлетворяют всем ограничениям и предположениям, принятым в задаче.
Целевая функция y =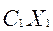 
+ 
+ 
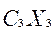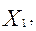
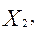
является линейной по переменным ( 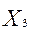) и, следовательно, достигает своего наибольшего и наименьшего значения на концах построенного отрезка, один из которых и является решением задачи.
