2015-04-01
698
2.2.1 Построение следов плоскости.
Для построения следов плоскости достаточно определить следы двух прямых линий (отрезков), принадлежащих этой плоскости. Рассмотрим построение следов прямой g на эпюре Монжа (смотри рисунок 2.1). Для решения этой задачи пользуемся следующим алгоритмом:
- чтобы найти горизонтальный след М прямой g сначала необходимо найти его фронтальную проекцию М2 как точку пересечения фронтальной проекции g2 прямой g с осью;
- недостающая горизонтальная проекция М1 совпадает с горизонтальным следом прямой g, то есть М≡М1;
- для нахождения фронтального следа N прямой сначала находим его горизонтальную проекцию N1, как точку пересечения горизонтальной проекции прямой g с осью;
- недостающая фронтальная проекция N2 совпадает с фронтальным следом N, то есть N ≡ N2
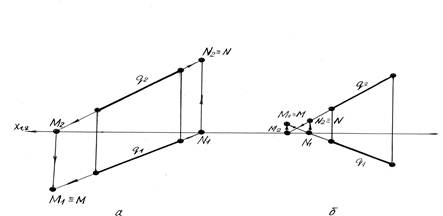
Рисунок 2.1
2.2.2 Определение угла наклона плоскости к плоскостям П1 и П2.
Прямые линии наибольшего наклона плоскости к плоскостям проекций П1 и П2 перпендикулярны соответственно горизонталям или фронталям этой плоскости. Рассмотрим случай определения угла наклона плоскости Σ, заданной прямой а и точкой С к горизонтальной плоскости проекций. Прямой угол, составленный линией наибольшего ската плоскости с ее горизонталью проецируется на горизонтальную плоскость проекций П1 без искажений. Для решения данной задачи (смотри рисунок 2.2):
- проведем через точку С горизонталь h (h1, h2);
- из любой точки, принадлежащей прямой а, восстанавливаем перпендикуляр к горизонтали h. Получаем А1К1 и А2К2 проекции перпендикуляра (А1К1 ┴ h);
- натуральную величину отрезка АК и угол его наклона к плоскости П1 находим по методу треугольника (смотри рисунок 2.2).
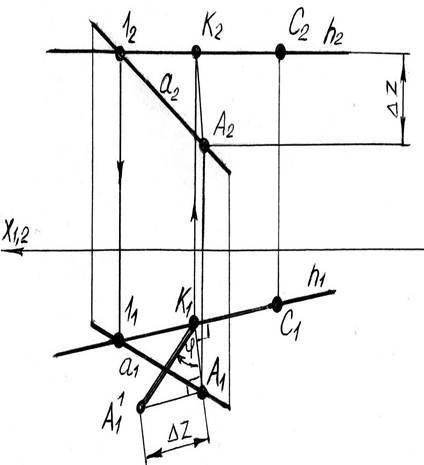
Рисунок 2.2
Как найти угол наклона плоскости к фронтальной плоскости проекций смотри на рисунке 2.3
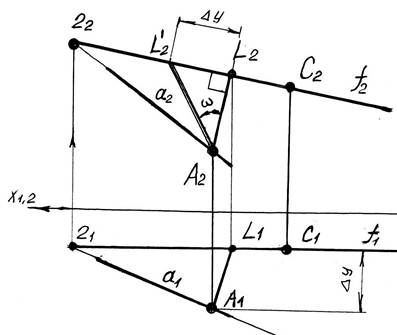
Рисунок 2.3
2.2.3 Определение натуральной величины треугольника методом вращения.
При решении метрических задач связанных с определением истинных размеров изображенных на эпюре (комплексном чертеже) фигур, могут встретиться значительные трудности, если заданные проекции не подвергнуть специальным преобразованиям. Для этой цели обычно применяют один из двух способов: вращения или замены плоскостей проекций. Для решения задачи по определению натуральной величины треугольника воспользуемся способом вращения его вокруг одной оси. Если задаться целью: одним поворотом расположить треугольник параллельно плоскости П1, то за ось вращения следует принимать такую в плоскости треугольника, которая еще до вращения была бы параллельна горизонтальной плоскости проекций, то есть одну из ее горизонталей (смотри рисунок 2.4).
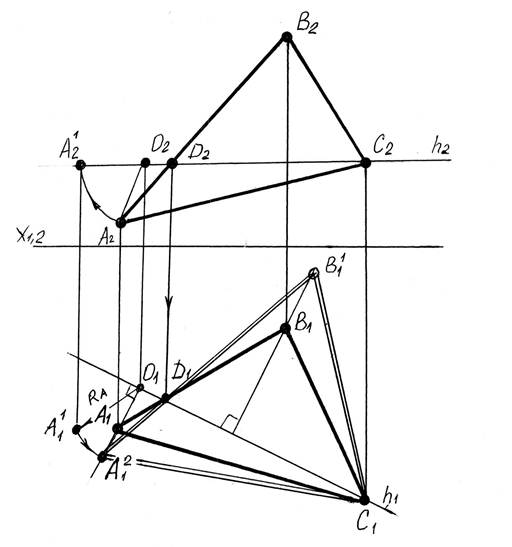
Рисунок 2.4
Построения выполняются в следующей последовательности:
- через точку С проведем горизонталь h (h2║ х1,2);
- из точек А1 и В1 восстанавливаем перпендикуляры к h1;
- строим проекции радиуса вращения одной из них (например А), это будут проекции А1О1 и А2О2;
- по двум проекциям определяем истинную величину радиуса вращения RА. В настоящем примере радиус определен методом вращения (его также можно определить методом треугольника);
- отрезок RА откладываем от точки О вдоль той прямой, по которой перемещается горизонтальная проекция вершины А;
- через полученную точку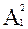 
и неподвижную D1 проводим прямую до пересечения с прямой, по которой перемещается горизонтальная проекция вершины В и на их пересечении отмечаем точку 
;
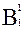- соединяя найденные точк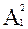и и 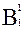друг с другом и с неподвижной вершиной С1, получаем горизонтальную проекцию треугольника. Эта проекция определяет натуральную величину треугольника АВС;
- фронтальная проекция треугольника окажется преобразованной в прямую линию, совпадающую с С2D2.
2.3 Указания к выполнению задания:
- по координатам точек А, В и С, взятым с таблицы 2.1 по вариантам, изображаем комплексный чертеж плоскости Σ(АВС), при этом выбираем ось х, начало координат и масштаб так, чтобы изображение заняло большую часть поля чертежа (смотри приложение Е);
- для построения следов плоскости Σ(АВС) находим горизонтальные и фронтальные следы двух прямых (отрезков) плоскости Σ. В нашем примере выбираем отрезки СВ и СА. Как определить следы прямых смотри теоретический раздел 2.2.1;
- найдя горизонтальные и фронтальные следы двух прямых, соединяем одноименные прямой и получаем следы плоскости;
- определяем углы наклона плоскости Σ(АВС) к плоскостям П1 и П2 (смотри раздел 2.2.2). В нашем примере горизонталь и фронталь проведены через точку А.
Контрольные вопросы.
2.4.1 Что мы называем следом плоскости и как его определить на комплексном чертеже.
2.4.2 Как определить углы наклона плоскости к плоскостям проекций.
2.4.3 Определение натуральной величины треугольника методом вращения.
