2015-04-17
2255
Измерение скорости в авиационных радиосистемах базируется на том факте, что два гармонических колебания, а именно, излученное в направлении движущегося объекта и отраженное от этого объекта (рис. 3.34) будут, в общем случае, иметь неодинаковые частоты. Разность данных частот называется доплеровской частотой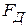 
, которая вычисляется следующим образом:
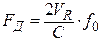, (3.36)
где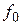 
– частота излученного гармонического колебания; 
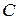– скорость распространения электромагнитных волн (3*108 м/с); 
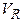– радиальная скорость объекта. При этом частота 
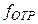гармонического колебания, отраженного от движущегося объекта, рассчитывается как 
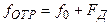, если объект удаляется, и как 
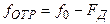, если объект приближается.
Что касается радиальной скорости 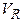, то она для точечного объекта, обладающего скоростью 
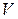, определяется как проекция величины 
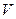на направление «объект – измерительная радиосистема».
Следуя геометрическому построению, приведенному на рис. 3.34, величина радиальной скорости определяется по формуле:
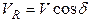, (3.37)
где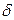 
– угол между вектором скорости 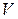и направлением «объект – измерительная радиосистема».
 |
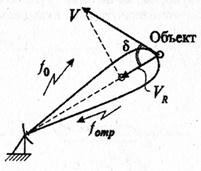Рис. 3.34. Геометрическое построение для нахождения радиальной скорости  |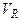
Возможен и иной вариант – гармоническое колебание частоты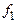 
излучает сам движущийся объект, а измерительная радиосистема выполняет лишь приемные функции. В таком случае, на вход измерительной радиосистемы поступит гармоническое колебание частоты 
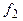, причем доплеровская частота 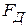, равная разности частот 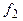и (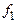
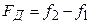), будет вычисляться согласно соотношению:
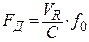. (3.38)
Величина доплеровской частоты 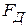много меньше, чем частота 
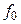излученного колебания. Так, например, если 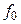=10 ГГц=1010 Гц (случай, типичный для радиолокационной практики), а 
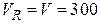м/с, то доплеровска частота 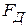, рассчитанная по алгоритму (3.36), будет равна 2*104 Гц=20 кГц.
Рассмотрим. механизм вычисления доплеровской частоты 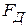для различных ситуаций, когда доплеровская измерительная приемо-передающая радиосистема установлена на борту самолета, движущегося горизонтально (в плоскости, параллельной земной поверхности) со скоростью 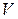: - ситуация 1 – ветер отсутствует; луч радиосистемы, направленный на землю под углом 
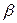, расположен в вертикальной плоскости, проходящей через осб фюзеляжа (рис. 3.1.34, а):
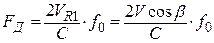(3.39)
- ситуация 2 – ветер отсутствует; луч радиосистемы, направленный на землю под углом 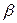, расположен вертикальной плоскости, которая отклонена на угол α относительно вертикальной плоскости, проходящей через ось фюзеляжа (рис. 3.1.34, б):
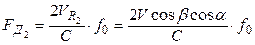(3.40)
- ситуация 3 – присутствует горизонтальный ветер, скорость которого векторно складываясь со скоростью самолета, создает новый вектор скорости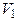 
, составляющий угол 
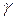(угол сноса) с осью фюзеляжа; прочие условия – те же, что и в ситуации 2; тогда значение 
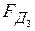будет (рис. 3.1.34, в):
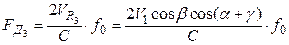(3.41)
 |
Рис. 3.35. Различные ситуации формирования радиальной скорости 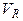 (самолет выполняет горизонтальный полет): а – вид сбоку; б и в – вид сверху |
Из анализа соотношения (3.41) видно, что по измеренной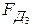 
невозможно одновременно вычислить однозначные значения скорости 
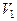и угла сноса 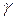. Эта неоднозначность проявляет себя в еще большей степени, когда полет самолета не происходит в горизонтальной плоскости и когда необходимо одновременно определять величины пространственных составляющих итогового вектора скорости совместно с углами сноса, крена и тангажа лишь по измеренной доплеровской части 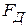. Чтобы избежать подобной неоднозначности; на самолетах и вертолетах устанавливают не однолучевые, а многолучевые (чаще всего трех- и четырех лучевые) доплеровские измерители скорости.
