Тема 5. Средние величины

Средняя величина является обобщающей характеристикой изучаемой совокупности, показывающей типичный уровень варьирующего признака в расчете на единицу совокупности.

Средние величины, используемые в статистике, относятся к двум классам: степенные и структурные средние.

Среди степенных средних в статистическом анализе наибольшее применение нашли:

1) Средняя арифметическая простая

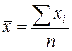
где 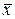– средняя арифметическая; х_i – отдельные варианты признака; n – количество групп.

Средняя арифметическая простая используется в том случае, если у всех группировочных признаков равны между собой частоты признака.

2) Средняя арифметическая взвешенная – используется если частоты признака не равны между собой

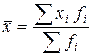
3) Средняя гармоническая взвешенная используется при отсутствии данных о частотах признака, (F = x*f) и вариантами признака (х)

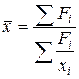
4) Средняя гармоническая простая используется в том случае если у всех вариантов признака равны между собой объемы признака (F=const)

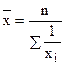
5) Средняя квадратическая ()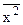

простая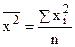

взвешенная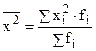

6) Средняя геометрическая ()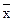

простая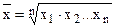

взвешенная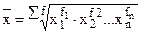

Основные свойства средней арифметической:

1) Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие частоты:

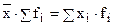
2) Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю:

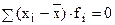
3) Если из всех вариантов признака вычесть одно и то же число, то средняя уменьшится на это число.

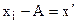
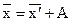
где А – произвольное число.

4) Если все варианты признака разделить на одно и то же число, то средняя уменьшится в это число раз.

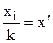
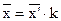
где k – произвольное число.

5) Средняя арифметическая может быть рассчитана методом условного нуля (методом моментов) при котором данные преобразуются до образования нуля последовательными операциями вычитания и деления вариантов признака на определенные числа (А и К)

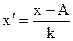
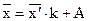
К структурным средним, наиболее часто используемым статистикой относят Моду и медиану.

Мода (Мо) – это значение признака, наиболее часто встречающегося в данном ряду.

В дискретном ряду распределения моду определяют по наибольшей частоте.

В интервальном ряду распределения мода определяется по формуле:

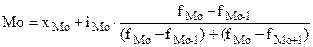
где 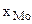- нижняя граница модального интервала; 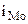- величина модального интервала; 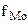- частота модального интервала; 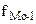- частота интервала, предшествующего модальному; 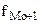- частота интервала, следующего за модальным.

Модальный интервал выбирается по максимальной частоте в исследуемом ряду распределения.

Медиана (Ме) – это значение признака, которое приходится на середину ранжированного ряда распределения.

Ранжированный ряд распределения представлен значениями всех признаков в порядке возрастания.

Порядковый номер признака в ранжированном ряду распределения определяется по сумме накопленных частот (кумулятивным частотам).

В дискретном ряду распределения медиана определяется исходя из условий:

Если в вариационном ряду 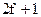случаев (нечетное число), то значение признака у случая 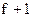будет медианным, т.е.

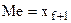Если в вариационном ряду 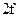случаев (четное число), то медиана равна средней арифметической из двух серединных значений.

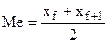
В интервальному ряду распределения медиана определяется по формуле:

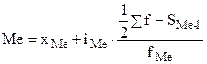
где 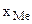- начало медианного интервала; 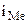- величина медианного интервала; 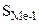- сумма накопленных частот до медианного интервала; 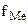- частота медианного интервала.