В процессе измерения между объектом и СИ устанавливается определенное взаимодействие, в результате которого возникает определенная реакция СИ. И взаимодействие, и реакция возможны только на основе некоторого материального носителя. Измерительная информация всегда проявляется в материально-энергетической форме в виде сигналов [8].
Передача информации об измеряемой величине от объекта к приемнику информации по отдельным преобразующим элементам измерительной системы осуществляется также сигналами. Материальную основу сигнала составляет какой-либо физический объект или процесс, называемый носителем информации. В качестве носителей измерительной информации чаще всего используются колебания различной природы: электромагнитные, упругой среды, оптические, тепловые, ионизационных излучений. Наибольшее распространение получили носители в виде электрического напряжения или тока.
Носитель становится сигналом в процессе модуляции.
Параметры носителя, изменяемые во времени в соответствии с законом изменения измеряемой ФВ, называют информативными. Например, при использовании гармонических электрических колебаний информативными могут быть такие параметры, как амплитуда, частота, фаза; при использовании периодического прямоугольного сигнала информативными могут быть амплитуда, частота следования импульсов, длительность импульса, скважность и т. д.
Таким образом, измерительным называют сигнал, обладающий информативными параметрами, содержащими информацию о значении измеряемой величины. Сигналы измерительной информации для обеспечения возможности соединения отдельных функциональных элементов ИС должны обладать совместимостью по роду, размеру информативных параметров, закону их изменения и т. д. Эта совместимость обеспечивается стандартизацией сигналов.
В процессе измерения информация должна быть выделена из входного сигнала оптимальным образом. Для этого необходимо рассмотреть свойства сигналов и их параметров, особенности входных и выходных сигналов СИ, математические модели сигналов.
Измерительные сигналы можно разделить на постоянные и переменные во времени, неслучайные и случайные, импульсные, стационарные, периодические и почти периодические.
Неслучайные сигналы подразделяются на детерминированные и квазидетерминированные. Детерминированный сигнал — это сигнал, закон которого известен, следовательно, известны и значения всех его параметров с определенной степенью точности. Детерминированные сигналы подают на входы СИ при их градуировке и поверке, используют в качестве несущих сигналов при передаче.
Квазидетерминированный сигнал — это сигнал с известным характером закона изменения во времени, но неизвестным по значению одним или несколькими параметрами. Неизвестный информативный параметр квазидетерминированпого процесса может иметь любые значения в весьма широком диапазоне и. может являться случайной величиной.
Случайным называют сигнал, значение которого в каждый момент времени является случайной величиной.
Сигналы, действующие на входе и выходе СИ, в зависимости от числа размеров, которые может иметь их основной параметр х, и характеристики изменения во времени можно разделить на аналоговые, дискретные, квантованные и цифровые (рис. 6.2).
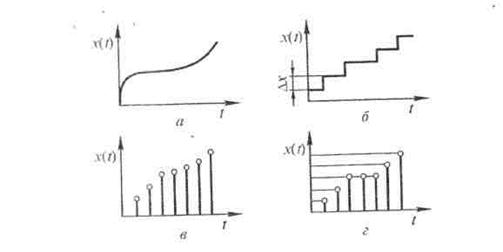
Рис. 6.2. Классификация сигналов: а — аналоговый; б — квантованный; в— дискретный: г — цифровой
Аналоговые сигналы задаются по оси времени несчетным множеством точек. Они произвольные по значению и непрерывные по времени.
Сигналы, дискретные по уровню, называются квантованными. Они принимают лишь дискретные значения, но непрерывные по времени, т. е. задаются на всей временной оси.
Дискретные сигналы задаются на дискретных значениях времени (на счетном множестве точек). Они произвольные по значению и дискретные по времени.
Цифровые сигналы — сигналы, дискретные по времени и квантованные по уровню. Используются для представления сигналов в цифровой форме с помощью цифрового кодирования, поскольку уровни можно пронумеровать числами с конечным числом разрядов.
Чтобы сделать сигналы объектами теоретического изучения и расчетов следует указать способ их математического описания, т. е. создать математическую модель сигналов.
Сигналы различного физического рода описываются общими математическими моделями (функциями):
х = ƒ(t, а, b, с...),
где х — основной параметр сигнала; а, b, с —другие параметры сигнала.
Таким образом, во временной области измерительный сигнал рассматривают как функцию времени, характеристики которой содержат информацию.
Рассмотрим наиболее типичные сигналы.
Импульсным называют сигнал, величина которого ничтожно мала в любой точке временной оси, за исключением некоторой конечной области.
Среди импульсных сигналов характерными являются приведенные на рис. 6,3.
Информативными параметрами импульсных сигналов являются значение сигнала, как функция времени х(t), амплитудное (максимальное) значение max{x(t)}), длительность сигнала т,
Для единичного и Гауссова сигналов площадь S=1.
Сигналы, значения которых повторяются через постоянные интервалы времени Т (периоды), называются периодическими (рис. 6.4).
Для периодических сигналов справедливо соотношение
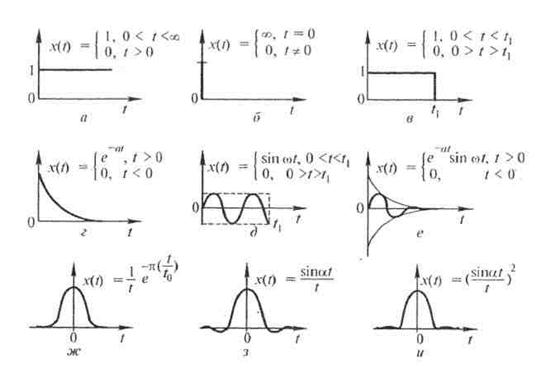
Рис. 6.3 Импульсные сигналы
а — единичная функция; б —единичный импульс (5-функция Дирака); в —прямоугольный; г— экспоненциальный; д— пакет синусоид; е — затухающая синусоида; ж — Гауссов импульс; з — импульс типа (sin /)//; и — импульс типа [(sin t)/!\2
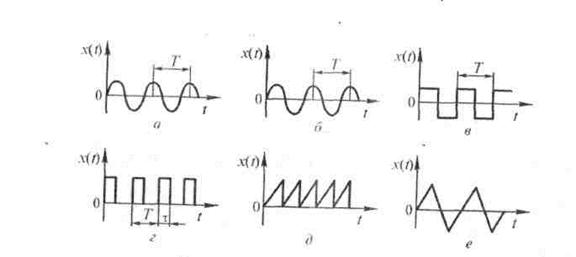 |
X(t) = x(t+kT), k = 0, +/-1, +/-2
К периодическим сигналам относится гармонический сигнал, для которого
X(t) = x0 cos (ω0t+φ0),
Где x0, ω0, φ0 – амплитуда, частота, фаза соответственно.
Периодический сигнал может быть представлен рядом Фурье
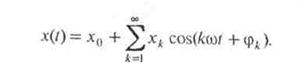 |
При этом параметры xk, ωk, φk могут быть информативными.
В измерительной технике широко применяются периодические последовательности прямоугольных импульсов, свойства которых определяются амплитудой хm, периодом повторения Т и деятельностью τ (рис. 6,4, в,г). Применяются так же пилообразные (рис.6.4,д) и треугольные импульсы (рис 6.4, е).
Для периодических сигналов рассматривают среднее значение за период
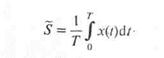 |
И среднюю мощность
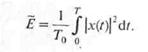 |
 2015-04-01
2015-04-01 6303
6303
