1. На листе Графики построить графики функций, приведенных ниже, используя диаграмму типа График и Точечную диаграмму. Результаты сравнить.
a) y=x^3+2x^2+2
b) y=sin x
c) y= -6x^2+3x
d) y=1/x
e) y=ln(x-1)+5
f) y=|cos x|
g) y=|x|+3
h) 3+2/(x-4)
i) y=1/(x^2+2x+1)
Результат сохранить в файле с именем Лабораторная работа №5.
2. Для таблицы, сформированной на листе "Преступность и судимость" в файле Лабораторная работа №2, по данным ее первого, второго, третьего и пятого столбцов построить графики, отражающие динамику основных криминологических показателей в России за 1985 – 1997 годы. Изменить на каждом графике маркеры значений данных и установить для каждого графика свою толщину линии.
3. Для таблицы, сформированной на листе "Торговля_и_Производство" в файле Лабораторная работа №2, выполнить следующие задания:
a) используя данные Год, Торговля, Производство за последние 10 лет, построить объемную гистограмму на отдельном листе с именем Развитие торговли;
b) отредактировать диаграмму:
- изменить подтип гистограммы, чтобы ряды данных размещались один перед другим;
- вставить основную сетку по всем трем осям диаграммы;
- сместить легенду под область построения диаграммы;
- ввести заголовок "Развитие торговли по отношению к производству за последние 10 лет";
- изменить данные в некоторой строке и посмотреть, что произойдет с диаграммой;
- вставить в таблицу новую строку и посмотреть, что произойдет с диаграммой;
c) по данным "Год" и "Доля" торговли построить круговую диаграмму на отдельном листе с именем "Доля_Торговли";
d) отредактировать диаграмму:
- нанести на диаграмму показатели значений к каждому участку диаграммы;
- выдвинуть участок круговой диаграммы, соответствующий самому большому значению Доли торговли.
4. Для таблицы "Продажа видеофильмов", сохраненной в файле Лабораторная работа №2, выполнить следующие задания:
- построить объемную гистограмму с накоплением "Продажа видеофильмов за первые 3 дня по категориям" (по оси категорий – категории фильмов, по оси значений – число продаж по дням);
- построить круговую диаграмму "Продажи за 6 января 1998 года", отображающую итоги продажи видеофильмов за 6 января 1998 года;
Результат сохранить в файле с именем Лабораторная работа №5.
Следующие задания выполняются по вариантам.
Номер варианта выполняемого задания совпадает с номером по списку группы (если номер по списку >10, то отнять от номера число 10, если номер по списку >20, то отнять от номера число 20).
Вариант 1
1. Построить в разных системах координат при 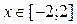 графики функций:
графики функций:
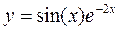

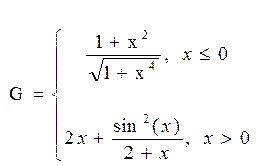

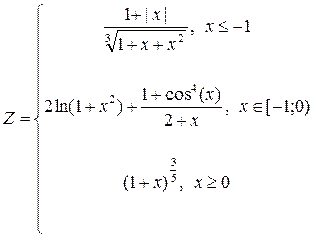
2. Построить в одной системе координат при 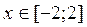 графики функций:
графики функций:
· Y=2sin(x)cos(x);
· 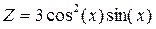 .
.
3. Построить поверхность 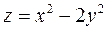 при
при 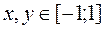 .
.
Вариант 2
1. Построить в разных системах координат при 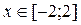 графики функций:
графики функций:
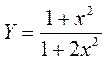
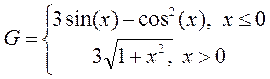
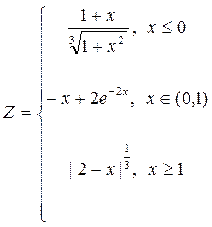
2. Построить в одной системе координат при 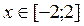 графики функций:
графики функций:
4. 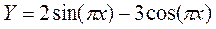
5. 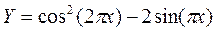 .
.
3. Построить поверхность 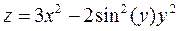 при
при 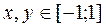 .
.
Вариант 3
1. Простроить в разных системах координат при 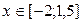 графики функций:
графики функций:
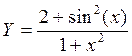
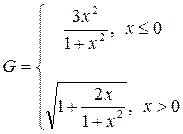
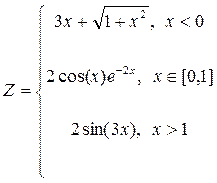 .
.
2. Построить в одной системе координат при 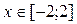 графики функций:
графики функций:
· 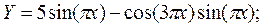
· 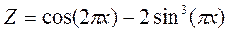 .
.
3. Построить поверхность 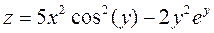 при xÎ[-1;1].
при xÎ[-1;1].
Вариант 4
1. Построить в разных системах координат при x 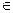 [-1,5;1,5] графики функций:
[-1,5;1,5] графики функций:
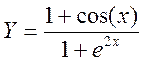
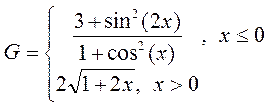
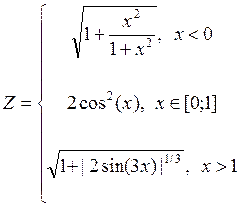
 .
.
2. Построить в одной системе координат при x 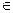 [-2;2] графики функций:
[-2;2] графики функций:
· Y = 3sin(2 πx) cos(πx) – cos2 (3πx);
· Z = 2cos2(2πx) – 3sin(3πx).
3. Построить поверхность при x, y 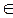 [-1;1]
[-1;1]
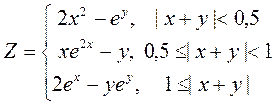 .
.
Вариант 5
1. Построить в разных системах координат при x 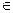 [-1,8;1,8] графики функций:
[-1,8;1,8] графики функций:
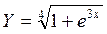
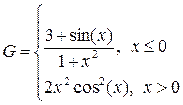

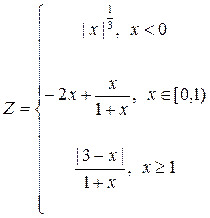
2. Построить в одной системе координат при x 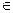 [0;3] графики функций:
[0;3] графики функций:
· Y = 2sin(πx)cos(πx);
· Z = cos 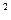 (πx)sin(3πx).
(πx)sin(3πx).
3. Построить поверхность 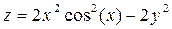 при x, y
при x, y 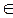 [-1;1].
[-1;1].
Вариант 6
1. Построить в разных системах координат при x 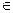 [-2;1,8] графики функций:
[-2;1,8] графики функций:
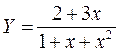
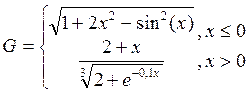
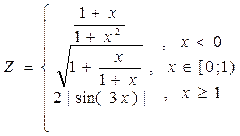 .
. 
2. Построить в одной системе координат при x 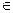 [-3;0] графики функций:
[-3;0] графики функций:
· Y = 3sin(3πx)cos(2πx);
· Z = cos3(4πx)sin(πx).
3. Построить поверхность 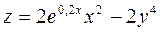 при x, y
при x, y 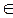 [-1;1].
[-1;1].
Вариант 7
1. Построить в разных системах координат при x 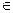 [-1,7;1,5] графики функций:
[-1,7;1,5] графики функций:
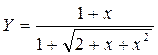
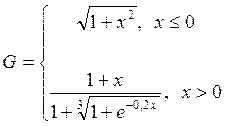
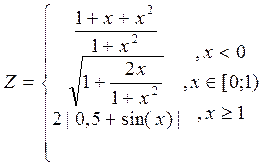
 .
.
2. Построить в одной системе координат при x 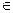 [-3;0] графики функций:
[-3;0] графики функций:
· Y = 2sin(2πx)cos(4πx);
· Z = cos2(3πx) – cos(πx)sin(πx).
3. Построить поверхность 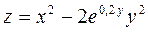 при x, y
при x, y 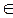 [-1;1].
[-1;1].
Вариант 8
1. Построить в разных системах координат при 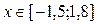 графики функций:
графики функций:
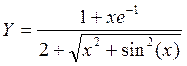
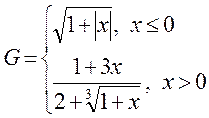
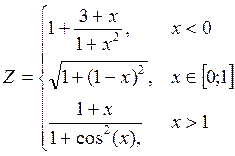 .
.
2. Построить в одной системе координат при 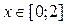 графики функции:
графики функции:
· 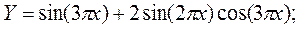
· 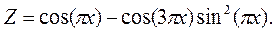
3. Построить поверхность при 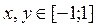
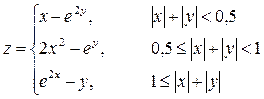
Вариант 9
1. Построить в разных системах координат при xÎ[1,4;1,9] графики функций:
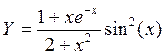
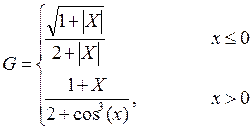


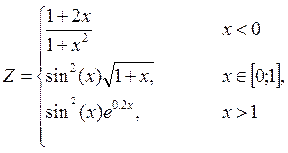
2. Построить в одной системе координат при хÎ[0;2] графики функций:
· 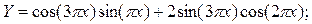
· 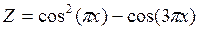 .
.
3. Построить поверхность при хÎ[-1;1]
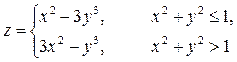 .
.
Вариант 10
1. Построить в разных системах координат при 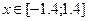 графики функций:
графики функций:
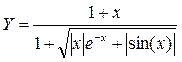
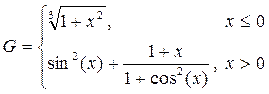
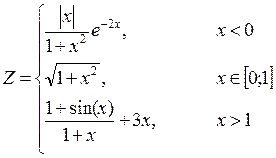
2. Построить в одной системе координат при 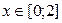 графики функций:
графики функций:
· 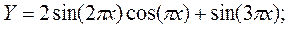
· 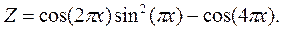
3. Построить поверхность 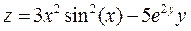 при
при 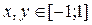 .
.
 2015-04-01
2015-04-01 2427
2427
