Сочетание изгиба и кручения стержней круглого сечения чаще всего встречается при расчете валов. При одновременной деформации изгиба с кручением внутренние усилия в поперечном сечении стержня приводятся к пяти компонентам: крутящему моменту 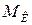 относительно оси
относительно оси 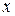 (рис. 34), изгибающим моментам
(рис. 34), изгибающим моментам 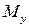 и
и 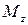 и поперечным силам
и поперечным силам 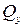 и
и 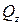 . Нормальные напряжения достигают наибольшего значения в крайних волокнах стержня (точки А и В, рис. 35), лежащих на концах диаметра, перпендикулярного к вектору результирующего изгибающего момента:
. Нормальные напряжения достигают наибольшего значения в крайних волокнах стержня (точки А и В, рис. 35), лежащих на концах диаметра, перпендикулярного к вектору результирующего изгибающего момента:
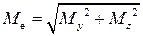 ;
; 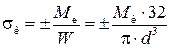 .
.
Касательные напряжения, определяющие 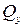 и
и 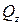 , незначительны и их при расчете обычно не учитывают.
, незначительны и их при расчете обычно не учитывают.
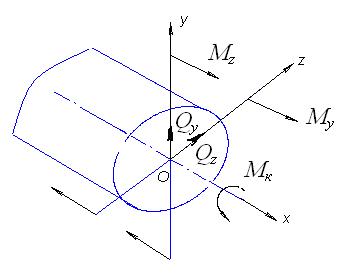
Рис. 34. Внутренние усилия в поперечном сечении
при одновременном действии деформации изгиба с кручением
Касательные напряжения от кручения достигают максимального значения во всех точках контура сечения.
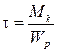 , или
, или 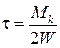 , так как для круглого сечения Wp = 2∙W
, так как для круглого сечения Wp = 2∙W
(Wp – полярный, W – осевой моменты инерции сечения).
В опасных точках А и В главные нормальные напряжения 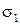 и
и 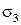 определяют по формуле
определяют по формуле 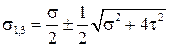 , а для проверки на прочность применяют одну из гипотез прочности.
, а для проверки на прочность применяют одну из гипотез прочности.
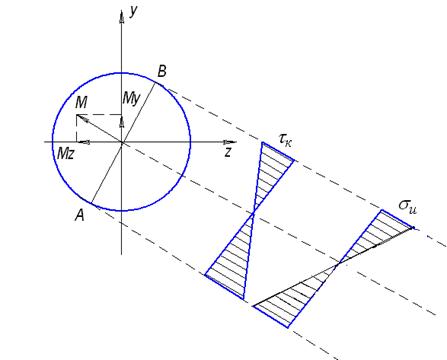
Рис. 35. Распределение касательных и нормальных напряжений
в поперечном сечении стержня при изгибе с кручением
Для пластичных материалов пользуются третьей или четвертой гипотезой прочности:
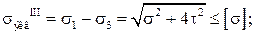
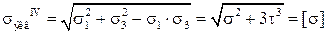 .
.
Для материалов, различно сопротивляющихся растяжению и сжатию, когда 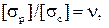 пользуются гипотезой Мора:
пользуются гипотезой Мора:
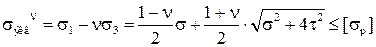 .
.
Выражая 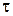 и
и 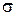 через крутящий и изгибающий моменты и подставляя значения главных напряжений в
через крутящий и изгибающий моменты и подставляя значения главных напряжений в 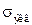 для различных теорий прочности, расчетные формулы приведем к виду
для различных теорий прочности, расчетные формулы приведем к виду
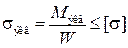 ,
,
где 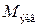 – эквивалентный (расчетный) изгибающий момент:
– эквивалентный (расчетный) изгибающий момент:
– по третьей теории прочности 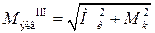 ;
;
– по четвертой теории прочности 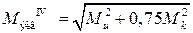 ;
;
– по теории Мора 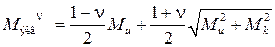 .
.
 2015-04-01
2015-04-01 1541
1541
