2015-01-30
4249
Эта деформация возникает в пространственных «ломанных» брусьях, в валах различных механизмов, передающие крутящие моменты. Здесь изгиб возникает от веса вала, веса шкивов, натяжения ремней, от зацепления зубчатых колес и т.д. Зная все нагрузки, можно построить все эпюры ВСФ. Опасное сечение определяется по эпюрам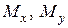 
и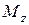 
. Как указано в разделе 6, брусья с некруглыми сечениями и тонкостенные незамкнутые сечения (двутавры, швеллера и т.д.), очень плохо работают на кручение. Поэтому, при наличии изгиба с кручением, желательно использовать брусья с круглыми или трубчатыми сечениями. Для них опасное сечение однозначно определяется по полному изгибающему моменту
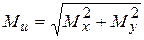(10)
Расчеты на прочность стержней, испытывающих изгиб с кручением, зависят от формы их поперечных сечений.
Расчет стержней круглого сечения
Для круглых стержней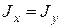 
и косой изгиб для них невозможен, поэтому расчет можно вести на 
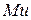, определяемый по (10). Плоскость изгиба перпендикулярна 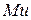(рис. 7.13) и
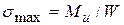(11)
 |
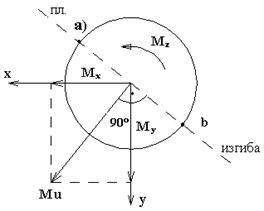Рис.7.13
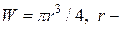радиус сечения. Знаки 
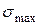зависят от направления вектора 
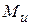. На рис. 7.13 в т. «а» будет сжатие (–), в т. «
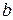» – растяжение 
. От кручения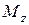 
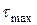, как известно, возникают на контуре сечения и определяются так 
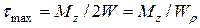(12) где 
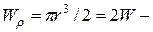полярный момент инерции сечения. Поэтому, наиболее опасными точками в сечении являются т. «а» и т. «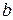», где действуют 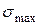и 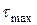и, следовательно, возникает плоское напряженное состояние (ПНС), которое излагается в разделе 12.
Главные напряжения при ПНС в осях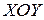 
определяются по (12.10)
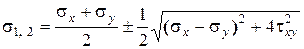(13)
В нашем случае надо подставлять: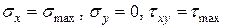 
из зависимостей (11), (12) и условие прочности запишется так
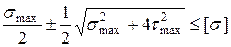(I)
А это, как известно, есть I теория прочности. (см. раздел 13)
Известны еще несколько теорий прочности, которые для ПНС в осях 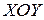записываются так (см. раздел 13):
II теория прочности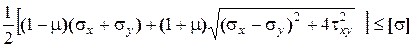 
.
В нашем случае подставляя: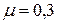 
(коэффициент Пуассона),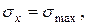 
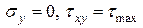получим
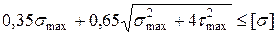(II)
III теория прочности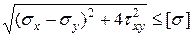 
В нашем случае
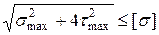(III)
IV теория прочности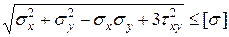 
В нашем случае
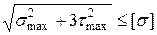(IV)
Формулы (I)-(IV) используются для проверки прочности валов с заданными размерами сечений. I и II теории прочности рекомендуются для валов из хрупких материалов (чугун), для которых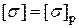 
(растяжение). III и IV теории прочности (т.п.) рекомендуется для валов из пластических материалов (стали и т.д.). При наличии в опасном сечении вала 
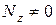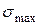, вычисляется с ее учетом
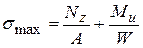(14)
Для проектирования вала, т.е. определения размеров его сечения, преобразуем формулы (I)-(IV): подставим формулы (11) и (12) в (I), получим
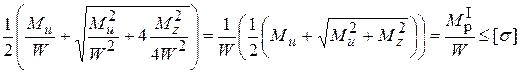
где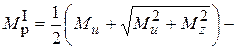 
расчетный (приведенный) момент по I теории прочности.
Подставляя (11) и (12) в другие теории прочности, легко убедится, что условия прочности I-IV можно записать одним обобщенным выражением
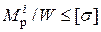(7.14)
где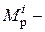 
расчетные моменты по 
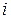ой теории прочности:
I т.п.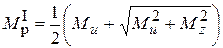 
;
II т.п.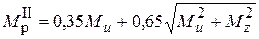 
; (7.15)
III т.п.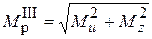 
;
IV т.п.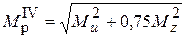 
Из условия прочности (7.14) можно найти необходимый момент сопротивления сечения вала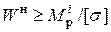 
, а по нему размеры сечения:
1. Сплошное круглое сечение радиуса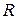 
: 
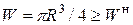, отсюда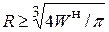 
2. Трубчатое сечение: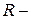 
наружный радиус, 
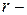внутренний. Здесь две неизвестных, а условие прочности (7.14) одно, поэтому надо самим задаться отношением 
. 
.
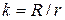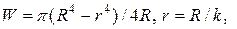
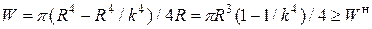Отсюда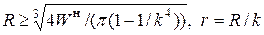 
.
Далее, по сортаменту труб подбираем стандартную трубу с близкими размерами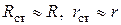 
, вычисляем 
, 
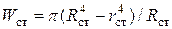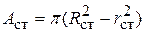, находим 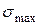по (14) и 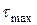по (12) и подставляем их в ту же теорию прочности (I)-(IV), по которой определялся 
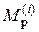из (7.15). Если условие прочности не выполняется, берем другую стандартную трубу и снова все повторяем. Допускаемая перегрузка 5% от 
.
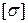Трубчатые сечения при изгибе с кручением являются более экономичными по весу.
Примечание: При наличии продольной силы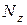 
размеры сечения определяются вначале без ее учета, т.е. на 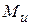и 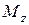, а проверка проводится с учетом 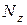по (14) и (12).
- Внутренние силовые факторы в пространственном «ломаном» стержне, построение их эпюр и определение опасных сечений.
