Пусть х * – искомое решение и сходящийся итерационный метод генерирует в процессе своей работы последовательность 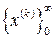 . Тогда будут справедливы следующие утверждения:
1. Метод сходится с линейной скоростью (или со cкоростью гео-метрической прогрессии, если для всех k, начиная с некоторого k * ³ 0 и 0 £ q < 1, выполнено условие
ç х (k + 1) – х *ê £ q ç х (k) – х *ê. (1.1.3)
2. Метод сходится со сверхлинейной скоростью, если для всех k, начиная с некоторого k * ³ 0, выполнено условие
ç х (k + 1) – х *ê £ qk ç х (k) – х *ê, (1.1.4)
где последовательность . Тогда будут справедливы следующие утверждения:
1. Метод сходится с линейной скоростью (или со cкоростью гео-метрической прогрессии, если для всех k, начиная с некоторого k * ³ 0 и 0 £ q < 1, выполнено условие
ç х (k + 1) – х *ê £ q ç х (k) – х *ê. (1.1.3)
2. Метод сходится со сверхлинейной скоростью, если для всех k, начиная с некоторого k * ³ 0, выполнено условие
ç х (k + 1) – х *ê £ qk ç х (k) – х *ê, (1.1.4)
где последовательность 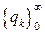 сходится к нулю.
3. Метод сходится с квадратической скоростью, если для всех k, начиная с некоторого k * ³ 0 и q ³ 0, выполнено условие
ç х (k + 1) – х *ê £ q ç х (k) – х *ê2. (1.1.5) сходится к нулю.
3. Метод сходится с квадратической скоростью, если для всех k, начиная с некоторого k * ³ 0 и q ³ 0, выполнено условие
ç х (k + 1) – х *ê £ q ç х (k) – х *ê2. (1.1.5)
|
Методы нулевого порядка, рассматриваемые в § 1.2 и 1.3, имеют следующие особенности.
1. Они ориентированы на исследование функции, унимодальной
на некотором начальном интервале 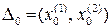 , содержащем искомую точку локального минимума.
, содержащем искомую точку локального минимума.
Начальный интервал D0 будем называть исходным интервалом неопределенности, длину этого интервала обозначим L 0. Определение интервала D0 осуществляется на первом (подготовительном) этапе, который называется этапом отделения (локализации) положения локального минимума. В зависимости от предполагаемых свойств минимизируемой функции для выполнения этого этапа используются различные способы, в том числе графические.
2. На втором этапе – этапе уточнения положения локального минимума – осуществляется последовательное уменьшение длины исходного интервала неопределенности, чтобы обеспечить требуемую точность вычисления оптимального решения х *.
Действительно, если известно, что х * Î 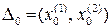 , то точка х 0 =
, то точка х 0 = 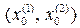 /2 (середина интервала) определяет значение х * с погрешностью, не превышающей L 0 / 2 – половины длины интервала неопределенности. Пусть теперь число e > 0 задает требуемую точность определения х *. Тогда если в процессе работы метода одномерной оптимизации длина текущего интервала Lk, содержащего х *, равна 2e, то требуемая точность определения будет достигнута, если в качестве х* выбрать точку
/2 (середина интервала) определяет значение х * с погрешностью, не превышающей L 0 / 2 – половины длины интервала неопределенности. Пусть теперь число e > 0 задает требуемую точность определения х *. Тогда если в процессе работы метода одномерной оптимизации длина текущего интервала Lk, содержащего х *, равна 2e, то требуемая точность определения будет достигнута, если в качестве х* выбрать точку 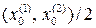 – среднюю точку текущего интервала неопределенности D k.
– среднюю точку текущего интервала неопределенности D k.
Таким образом, в процессе работы рассматриваемых методов итерационно строится некоторая последовательность вложенных интервалов неопределенности D i, i = 0, 2, 3, …, k, …:
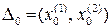 É D1 =
É D1 = 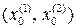 É … É D k =
É … É D k = 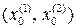 É …
É …
При этом если исходный интервал D0 содержит искомую точку х *,
то ее содержат и все остальные интервалы строящейся последовательности.
Работа метода завершается, когда длина очередного k -го интервала неопределенности окажется достаточно малой. Тогда искомую точку минимума определяют как середину последнего интервала неопределен-ности D k.
Построение последовательности вложенных интервалов базируется на свойстве унимодальности функции на начальном интервале неопределенности. Рассмотрим основное правило, позволяющее последовательно уменьшать длину этого интервала. Пусть 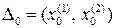 . Внутри этого интервала выберем каким-либо образом две точки – х 1, х 2, такие, что х 1 < х 2. Тогда возможны три случая (в силу унимодальности функции f (x)):
. Внутри этого интервала выберем каким-либо образом две точки – х 1, х 2, такие, что х 1 < х 2. Тогда возможны три случая (в силу унимодальности функции f (x)):
– если f (х 1) > f (х 2), точка минимума может быть только на интервале 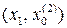 ;
;
– если f (х 1) < f (х 2), точка минимума может быть только на интервале 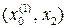 ;
;
– если f (х 1) = f (х 2), точка минимума может быть только на интервале (х 1, х 2).
Во всех случаях исходный интервал неопределенности уменьшился на некоторую величину, в результате чего был получен новый интервал D1, содержащий точку минимума. Этот интервал также может быть уменьшен аналогичным образом. Методы, которые будут рассмотрены ниже, отличаются друг от друга способом выбора на каждом шаге пробных значений х 1 < х 2 внутри текущего интервала неопределенности.
 2015-04-01
2015-04-01 589
589








