Определение 1.1.7. Достаточные условия оптимальности

(по второй производной)

Пусть точка x^* Î X – стационарная точка функции f (x), которая в некоторой окрестности x^* дважды непрерывно дифференцируема. Тогда x ^* Î X является точкой локального минимума функции f (x), если f ¢¢(x ^*) > 0.

Используя сформулированные необходимые и достаточные условия, поиск оптимального решения задачи (1.1.1) для случая дифференцируемой на множестве X функции f (x) можно осуществить, выполнив, например, следующие действия:

1. Определить множество стационарных точек функции f (x), принадлежащих множеству X.

2. Проверить в каждой стационарной точке выполнение достаточного условия минимума функции f (x) и вычислить ее значение в тех точках,
в которых это условие выполнено.

3. Из всех точек, в которых вычислялось значение функции[2], выбрать точку с наименьшим значением.

В заключение отметим характерные особенности рассмотренного метода решения задачи (1.1.1):

– он может быть практически реализован, если число стационарных точек функции f (x) на множестве X, определяемых в п. 1, и число граничных точек в случае замкнутого множества X, анализируемых в п. 3, конечно. В этом случае метод позволяет определить глобальный минимум функции f (x) на множестве X;

– в общем случае рассмотренный метод достаточно трудоемкий,
так как требует вычисления производных первого и, возможно, второго порядков в подозрительных на экстремум точках, число которых может быть очень велико;

– нахождение производных минимизируемой функции далеко
не всегда возможно в реальных задачах, часто функции не задаются аналитически.

В практическом отношении рассмотренный метод не имеет большой ценности, тем не менее многие известные методы решения задачи (1.1.1) используют необходимые условия экстремума в том смысле, что они ориентированы на поиск решения уравнения f^¢ (x) = 0, т. е. на поиск стационарных точек минимизируемой функции. Если это уравнение не может быть решено аналитически, то для его решения применяются численные методы. Для решения задачи (1.1.1) используются численные методы, которые могут быть классифицированы по различным характерным признакам.
В частности, если в качестве такого признака используется необходимость вычисления производных минимизируемой функции, все рассматриваемые в данном пособии методы можно разделить на две группы:

– методы нулевого порядка – их реализация не требует вычисления производных минимизируемой функции;

– методы второго порядка – их реализация требует вычисления производных второго порядка минимизируемой функции.

Рассматриваемые методы одномерной оптимизации являются итерационными. С их помощью, начиная с некоторого начального приближения х ⁽⁰⁾, строят 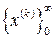– бесконечную последовательность точек х ⁽⁰⁾, х ⁽¹⁾, х ⁽²⁾, …, х ^(k), …, где х ^(k) – k -е приближение к искомой точке х ^* локального минимума функции f (x).