Основные понятия. К задачам многомерной безусловной оптимизации относятся задачи нахождения экстремума функции нескольких переменных без ограничения на возможные значения этих

К задачам многомерной безусловной оптимизации относятся задачи нахождения экстремума функции нескольких переменных без ограничения на возможные значения этих переменных. В общем случае задача состоит в том, чтобы отыскать x ^* Î E_n, для которого выполнено условие

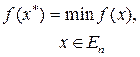(2.1.1)

где x = (x ₁, x ₂, …, x_n) ^т – вектор варьируемых параметров x ₁, x ₂, …, x_n;
n – размерность вектора х; f (x) – вещественная скалярная функция векторного аргумента или функция n- переменных; E_n – n- мерное евклидово пространство.

Как и для задач одномерной оптимизации, часто используется следующая терминология:

– f (x) – функция цели или целевая функция;

– " x Î E_n – решение задачи (2.1.1);

– x ^* – оптимальное решение задачи (2.1.1).

Задачу (2.1.1) называют задачей безусловной многомерной оптимизации, так как на значения компонент векторного аргумента x
не накладывается никаких условий.

Решить задачу (2.1.1) – значит найти ее оптимальное решение. Отметим, что, как и в случае задачи одномерной оптимизации,
для нахождения максимума функции j(x) достаточно взять функцию
f (x) = –j(x) и решить задачу по нахождению минимума функции f (x) на E_n. Поэтому рассмотрение задачи минимизации (2.1.1) не умаляет общности.

Методы многомерной безусловной оптимизации, как и методы одномерной безусловной оптимизации, являются итерационными. С их помощью строят 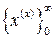– в общем случае бесконечную последовательность точек x ^{( k )} Î E_n, k = 0, 1, 2, …, сходящуюся при выполнении условий сходимости к x ^* Î E_n – точке, отвечающей оптимальному решению задачи (2.1.1). В дальнейшем последовательность 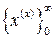, в которой каждый элемент х ^(k) Î E_n, k = 0, 1, 2, … является вектором, будем также называть векторной.