Метод 2

1. На отрезке [ a, b ] задать одномерную сетку

h _x = { x_i / x_i = x_{i – 1} + h_i, h_i > 0, i = 1, 2, 3, …, n; x ₀ = a, x_n = b }

и значения y_i = f(x_i) в узлах сетки x_i, i = 0, 1, 2, …, n.

2. Задать систему базисных функций j₀(х), j₁(х), j₂(х), j _m (х).

3. Вычислить j _k (х_i), k = 0, 1, 2, …, m; i = 0, 1, 2, …, n – значения базисных функций в узлах сетки h _x и в соответствии с (3.5.12) сформировать матрицу A.

4. Определить с = (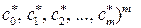 – вектор параметров модели (3.5.2) как обобщенное решение системы линейных уравнений (3.5.11). Решать систему (3.5.11) можно помощью одного из методов, использу-ющих ортогональные преобразования.

5. Модель j (х, 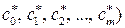, построенная согласно (3.5.2), является наилучшей в смысле МНК. Процесс завершен.

В заключение сделаем несколько замечаний по поводу рассмотренных методов.

1. В случае когда m – число модельных параметров будет равно n – количеству узлов сетки h _x, наилучшая в среднеквадратическом смысле модель j (х, 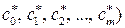будет интерполяционной.

2. Метод 1 может быть предпочтительней метода 2 при m << n.
В этом случае преимущество первого метода будет заключаться в небольшой размерности системы линейных уравнений (3.5.9) по сравнению с системой (3.5.11).

3. Метод 2, очевидно, будет предпочтительней метода 1 при
не очень хорошей или плохой обусловленности матрицы (3.5.12). В этом случае вычислительная устойчивость процесса будет в большей степени гарантирована при решении системы (3.5.11) без применения первой трансформации Гаусса.

В данной работе рассмотрена линейная задача, решенная методом наименьших квадратов. Довольно часто встречаются и нелинейные задачи МНК. Принципиально нелинейная задача решается аналогично линейной, но вместо линейных систем уравнений приходится решать нелинейные.

В целом следует отметить большую практическую значимость решения проблемы аппроксимации функций и МНК.

Глава 4. Численное дифференцирование
и интегрирование функций