Решение. Обозначим: А - событие, состоящее в том, что выиграна вещь, вероятность этого события

Обозначим: А - событие, состоящее в том, что выиграна вещь, вероятность этого события: .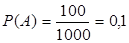

Событие В - выиграны деньги. Вероятность события В: .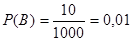

События А и В несовместные, так как один билет может выиграть либо вещь, либо деньги. Событие А+В состоит в выигрыше или вещи, или денег.

Согласно теореме сложения вероятностей для несовместных событий (1.3) находим: Р(А+В)=Р(А)+Р(В)=0,1+0,01=0,11.

Следствие 1. Если несовместные события А₁, А₂,…, А_n образуют полную группу, то сумма вероятностей этих событий равна единице, т. е.

P(А₁ + А₂ +…+ А_n) = P(А₁) + P(А₂) + …+ P(А_n)=1.

Следствие 2. Сумма вероятностей противоположных событий равна единице: .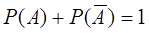

Например, вероятность появления "герба" при одном подбрасывании монеты равна ½, вероятность противоположного события – выпадения "решки": 1- ½ = ½.

Если события совместны, то при сложении вероятностей этих событий следует учитывать вероятность их совместного появления.

Теорема. Сложение вероятностей двух совместных событий. Вероятность суммы двух совместных событий равна сумме вероятностей этих двух событий без вероятности их совместного появления:

Р(А+В) = Р(А) + Р(В) - Р(АВ). (1.4)

1.6.Теорема умножения вероятностей

Различают зависимые и независимые события. Два события называются независимыми, если появление одного из них не изменяет вероятности появления другого. Например, если в цехе работают две автоматические линии, по условиям производства не связанные между собой, то остановки этих линий — независимые события.

События называют зависимыми, если появление одного из них изменяет вероятность появления другого. Вероятность одного события (В), вычисленная в предположении осуществления другого события (А), называется условной вероятностью события В. Обозначается Р(В/А) или Р_А(В) и читается: вероятность наступления события В при условии, что А произошло.

Теорема. Вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие произошло:

Р(АВ)=Р(А)Р(В/А), (1.5)

или Р(АВ)=Р(А)Р_А(В).

Вероятность произведения нескольких зависимых событий равна произведению вероятности одного из этих событий на условные вероятности других. Условная вероятность каждого последующего события вычисляется в предположении, что все предыдущие события произошли:

P(A₁ A₂ …A _{n -1} A _n)= P (A₁)·P (A₂ / A₁)·…·P(A _n / A₁ A₂ …A _{n -1}),

или P(A₁ A₂ …A _{n -1} A _n)= .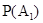

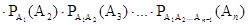Пример 1.3. Имеется 10 радиоламп, среди которых 3 неисправные, на вид не отличающиеся от новых. Наугад выбирают друг за другом две лампы. Какова вероятность того, что обе лампы окажутся исправными.

Решение. Пусть событие А₁ состоит в том, что первая лампа окажется исправной. Вероятность .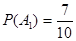

Событие А₂ – вторая лампа исправная. Вероятность второго события будет зависеть от события А₂.

.

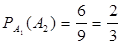Событие А₁А₂ состоит в том, что обе лампы исправны. Применяем теорему умножения вероятностей зависимых событий (1.5).

.

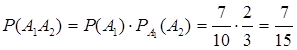Теорема. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий.

или Р(АВ)=Р(А)Р(В). (1.6)

Эта теорема может быть распространена на произвольное число событий, независимых в совокупности.

P(A₁ A₂ …A_n-1 A_n)= P(A₁)·P(A₂)·…P(A_n-1)·P(A_n).

Пример 1.4. Прибор состоит из двух узлов, которые во время работы могут независимо друг от друга выходить из строя. Пусть вероятность безотказной работы первого узла в течение гарантийного срока равна 0,7, а второго 0,9. Найти вероятность того, что в течение гарантийного срока прибор будет работать исправно.

Решение.

Прибор работает исправно, если его два узла работают без сбоев. Пусть событие А₁ состоит в том, то первый узел работает, Р(А₁)=0,7. Событие А₂ – второй узел работает, Р(А₂)=0,9.

Тогда, вероятность того, что оба узла работают, найдем по теореме умножения вероятностей независимых событий (1.6):

Р(А₁ А₂)= Р(А₁) Р(А₂)=0,7·0,9=0,63.

Пусть А – событие, состоящее в том, что появится хотя бы одно событие из событий А₁, А₂,…А_n. Событием, противоположным событию А, будет событие, состоящее в не появлении ни одного из этих событий, то есть событие .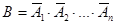

События А и Вобразуют полную группу. Поэтому

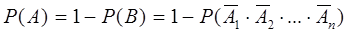. (1.7)

Пример 1.5. Студент знает20 вопросов из 40 по первому разделу и 40 из 50 вопросов по второму разделу. На экзамене ему случайным образом предлагается ответить на вопросы из обоих разделов. Найти вероятность того, что студент ответит правильно: 1) на оба вопроса; 2) только на один вопрос; 3) хотя бы на один вопрос.