Информационный расчёт ИИС

(Выбор частоты опроса датчика в ИК).

Для обработки сигналов с помощью ЦВМ они должны быть представлены в цифровой форме и для чего пройти этапы дискретизации, квантования и кодирования. Дискретное представление непрерывных сигналов есть процесс преобразования функции непрерывного времени 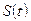в функцию дискретного времени 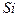, по значениям которых может быть выставлен сигнал 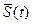оценка исходного непрерывного сигнала .

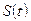Для восстановления непрерывных сигналов, представленных регулярными отсчётами широко применяется интерполяция.

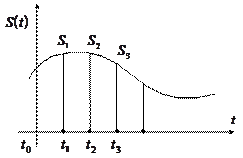В качестве интерполирующих функций чаще всего применяют полиномы, например если для восстановления измеряемого процесса S(t) рассматриваются его значения 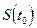, ,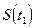..., 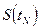в N+1 узлах (отсчётов), то аппроксимирующий степенной полином вида 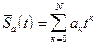должен проходить через все значения отсчётов, а следовательно удовлетворять следующим условиям:

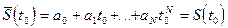
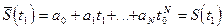
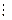
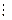
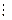
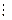
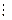
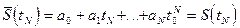
Решение этой системы может быть представлено в виде интерполяционного полинома Лагранж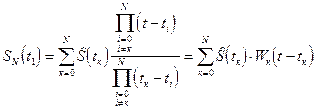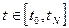а:

, (а)

где весовая функция 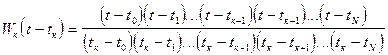(б)

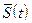– интерполирующая функция.

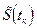– оценка значения отсчёта в момент 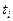с учётом его зашумлённости.

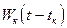– весовая функция (принимает значение 1 в одной узловой точке и 0 во всех других).

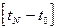– интервал интерполяции.

Нетрудно убедится, что выражение (а) является многочленом степени N, проходящим через N+1 точку. Полиномы Лагранжа широко используются на практике в следствии простоты реализации на ЭВМ. Чаще всего используют полиномы низких порядков, наиболее просто вычисляемые:

– нулевого порядка (ступенчатая интерполяция)

– первого порядка (линейная интерполяция).

При ступенчатой интерполяции (N=0) из общих формул (а) и (б) получим:

,

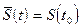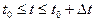
При линейной интерполяции (N=1) будем иметь:

, .

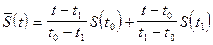Интерполяционные формулы Ньютона, Гаусса, Бесселя, Стирлинга и др. являются разновидностями интерполяционной формулы Лагранжа, которая часто неудобна тем, что в ней нельзя пренебречь ни одним слагаемым в отличие формулы Ньютона где в качестве слагаемых используются многочлены повышающихся степеней, позволяющие априори определить число слагаемых, требующих вычисления для достижения желаемой точности. Поэтому часто применяется интерполяционная схема Эйткина.

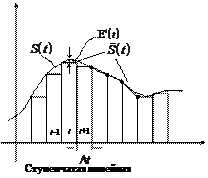Отклонение оценки 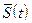от исходного измеряемого сигнала 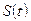или погрешность восстановления можно оценить различными показателями из которых, в основном, используются следующие:

1. Показатель наибольшего отклонения (равномерного приближения), характеризующий максимальное абсолютное значение погрешности восстановления на интервале наблюдения 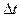по множеству реализаций: ,

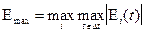где 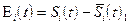– текущая погрешность восстановления, 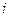– номер реализации.

Показатель обладает тем достоинством, что позволяет учесть все изменения восстановленного процесса, включая короткие выбросы. Показатель равномерного приближения используется при решении ряда задач анализа и синтеза различных устройств, которые имеют дело с обработкой текущих реализаций случайного процесса в реальном масштабе времени (например, устройств сжатия данных), а также в тех случаях, когда необходимо оценить предельные отклонения измеряемых параметров от номинальных значений.

Часто используют приведённое значение погрешности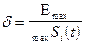

2. Показатель среднеквадратического приближения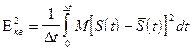

Выбор частоты дискретизации по этому критерию производится для стационарных измеряемых процессов с известной корреляционной функцией.

Полная погрешность восстановления сигнала, зависящая от способа интерполяции, определяется параметрами квантования сигнала во времени и по уровню, а именно: частотой дискретизации 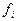и числом двоичных символов 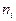, отводимых на кодирование одного отсчёта для i -го измерительного канала.

Важной информационной характеристикой измерительной системы является функция, называемая информационной производительностью измерительного канала: 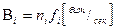, где ,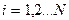

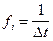
При проектировании системы стремятся обеспечить, по возможности, меньшее значение информационной производительности, поскольку это позволяет экономить на аппаратуре сбора, обработки и регистрации данных.

В общем виде задача выбора оптимальных параметров квантования достигается при выполнении 2-х условий, которые записываются следующим образом:

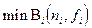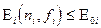1. ; 2. . (1)

здесь 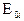допустимая погрешность восстановления сигнала; функция 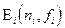показывает зависимость ошибки восстановления от параметров квантования. Вид этих функций показан в таблице 1.

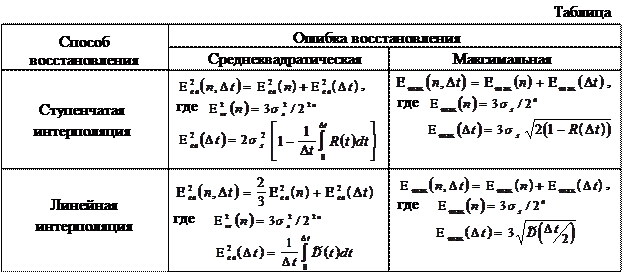Зависимость ошибки восстановления от параметров квантования

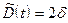
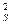
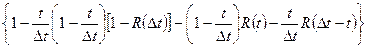
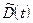­– дисперсия текущей ошибки восстановления сигнала

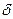
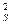­– дисперсия сигнала

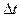– интервал дискретизации

В таблице приведены зависимости среднеквадратичной 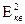и максимальной 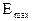ошибок восстановления сигналов способами ступенчатой и линейной интерполяции. Эти функции зависят от 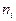и 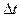параметров дискретизации, причем составляющие результирующей погрешност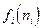и и 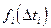являются функциями одного из параметров и суммируются между собой.

Алгоритм оптимального выбора параметров дискретизации сигнала задача (1) состоит из следующих этапов:

1. Согласно исходным данным подбирается функция .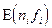

2. Из уравнения 2 условий (1) находится в явном виде зависимость .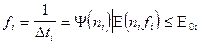

3. Определяется информационная производительность .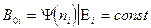

4. Находится значение 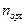, для которых 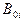– min.

5. Находится оптимальное значение частоты дискретизации .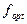

Нахождение выражений для 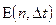из таблицы 1 достаточно трудоемкая задача. Мы в качестве примера рассмотрим нахождение составляющих погрешности для случая восстановления сигнала полиномом 0-ой степени (ступенчатая интерполяция при использовании критерия оценки точности восстановления – СКО).

Рассмотрим в выражении для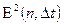

составляющую ошибки квантования – .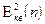

При равномерном квантовании шаг квантования 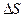– постоянный. Если процесс 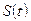стационарный, то шкала (динамический диапазон сигнала) 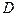для всех выборок одинакова, поэтому число уровней квантования 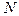не зависит от номера выборки: 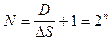, где 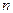– число разрядов бинарного кода.

Погрешность квантования является случайной функцией времени, вероятностные характеристики которых зависят от вероятностных характеристик процесса. В этом смысле погрешность квантования можно рассматривать как внешнюю аддитивную помеху 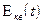(шум квантования). При малой допустимой погрешности квантования, когда 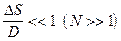шум квантования в различных выборках можно считать коррелированным, при этом можно ограничиться оценкой его одномерных вероятностных характеристик. Если началу шкалы соответствует уровень с номером 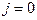, а концу шкалы уровень 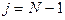и значение выборки отождествляется с ближайшим уровнем квантования или с серединой между соседними уровнями, то максимальная по модулю погрешность квантования:

; .

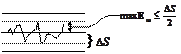
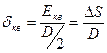При 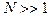, как это обычно бывает на практике изменением плотности вероятности значений выборки на интервале, равном шагу квантования можно пренебречь и считать, что она распределена равномерно.

Тогда

s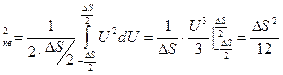

Откуда, считая сигнал нормально распределённым т.е.

s 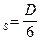(при равномерном распределении s )

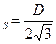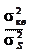
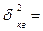
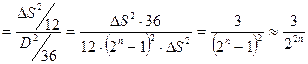
Откуда 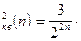s s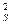

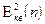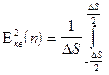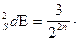Найдём , по определению: s s 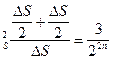s s ,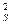

что и требовалось доказать.

Рассмотрим в выражении для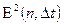

составляющую ошибки дискретизации –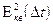

Рассматриваем как и в предыдущем случае пример равномерной дискретизации (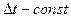) стационарного процесса 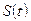с известной корреляционной функцией 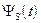. В качестве аппроксимирующей функции примем полином нулевой степени (ступенчатая интерполяция), при которой: , .

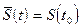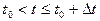В момент времени 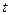текущая ошибка дискретизации равна:

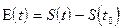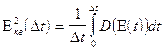; (1)

Дисперсия погрешности дискретизации при ступенчатой интерполяции выражается равенством 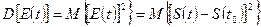. Раскрывая скобки и

учитывая, что у случайного стационарного эргодического процесса для случайной величины :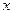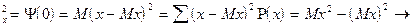

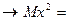s

s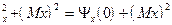

имеем:

,

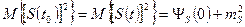
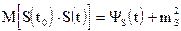где 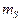– математическое ожидание 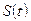, 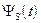– корреляционная функция для .

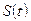Исходя из этого запишем формулу для 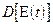в следующем виде:

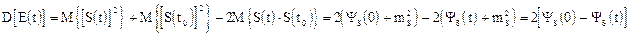
откуда из (1) и учитывая, что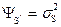

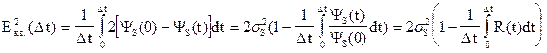
,где 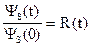- удельная корреляционная функция. Что и требовалось доказать.

Выражения для ошибок дискретизации и квантования для линейной интерполяции и критерия максимального отклонения, приведенные в таблице 1 здесь не доказываются, но при их определении используют подходы, аналогичные рассмотренным выше.