Практика аренды складских помещений, а также расчеты затрат на хранение на складах ряда фирм, говорят о том, что как правило учитывается не средний размер партии, а площадь (или объем) склада, которая требуется для всей поступившей партии. Таким образом затраты на хранение могут быть выражены формулой [27]:
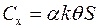 , (5.10)
, (5.10)
где a – затраты на хранение продукции в единицу времени с учетом занимаемой площади (объема) склада, руб./м2.ед. времени (руб./м3. ед. времени);
k – коэффициент, учитывающий пространственные габариты единицы продукции, м2/шт. (м3/шт.).
θ – коэффициент, учитывающий неодновременность поступления различных видов продукции на склад, 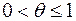 (примем θ= 1).
(примем θ= 1).
Коэффициент θ отражает преимущества современных технологий грузопереработки продукции на складах: по мере освобождения стеллажей (ячеек, площадей) на них размещаются вновь поступающие партии продукции, не дожидаясь момента окончания расхода предыдущей партии. В результате повышается наполняемость склада, что приводит к снижению затрат на хранение продукции.
С учетом выражения (5.10) формула Харриса-Уилсона (5.6) может быть преобразована следующим образом [27, 32]:
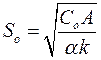 . (5.11)
. (5.11)
Величина минимальных затрат рассчитывается по формуле:
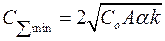 . (5.12)
. (5.12)
Полученные зависимости показывают, что в общем случае целесообразно представление затрат на хранение в виде двух составляющих
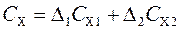 , (5.13)
, (5.13)
где 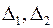 – коэффициенты, отражающие степень участия различных видов затрат на хранение, например,
– коэффициенты, отражающие степень участия различных видов затрат на хранение, например, 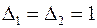 .
.
Один из возможных вариантов зависимости (5.12) может быть представлен в виде:
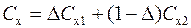 , (5.14)
, (5.14)
где Δ – коэффициент, 0≤Δ≤1.
Первая составляющая Cх1 отражает затраты, связанные со страхованием, учетом рисков, налогами и другими, определяемыми в зависимости от цены единицы товара и средней его величины. Вторая составляющая Cх2, отражающая затраты, связанные с хранением продукции, рассчитывается пропорционально площади (или объему), которую занимает поступивший заказ на складе. Таким образом, с учетом (5.13) зависимость (5.14) может быть представлена в виде:
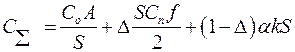 . (5.15)
. (5.15)
Формула (5.15) для удобства расчетов может быть представлена в виде:
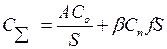 , (5.16)
, (5.16)
где 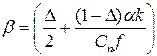 .
.
Пример 5.2:
Годовая потребность в заказываемом продукте (А)=1000 ед; затраты на выполнение одного заказа (С0) =500 руб. Каждая единица продукции, упакована в ящик следующих размеров: a x b x c (a = 0,3 м – ширина; b = 0,4м – длина; с = 0,3 м – высота); при хранении допускается штабелирование ящиков в h ярусов (h =6). Стоимость аренды склада составляет 270 руб./м2 в месяц. Определить параметры модели EOQ.
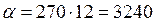 руб./м2год;
руб./м2год;
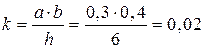 м2/ед;
м2/ед;
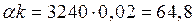 руб./ед. год.
руб./ед. год.
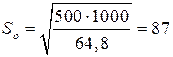 ед;
ед;
Минимальные затраты:
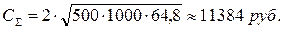
Количество заказов N = 12 и периодичность заказов Т з≈ 30 дней.
 2015-04-01
2015-04-01 3607
3607
