4.34. При расчете стен в процессе их возведения, а также сооружений, не имеющих верхней горизонтальной опоры (например, промышленных дымовых труб, подпорных стен и т. п.), кроме расчета на прочность и трещиностойкость необходима проверка на устойчивость положения стены или сооружения. Это относится к сечениям, в которых не могут быть восприняты растягивающие усилия, как, например, в уровне опирания фундамента на грунт, стены - на гидроизоляционный слой и т. п.
Цель расчета - предупредить опрокидывание конструкций при малой продольной и значительной поперечной силе. В этом случае опрокидывание может произойти при обмятии или незначительном выкрашивании одной лишь кромки сечения.
Устойчивость положения стены обеспечивается при условии, если равнодействующая горизонтальных и вертикальных сил находится в пределах сечения на достаточном расстоянии от его сжатого края, т. е. при ограничении величины эксцентриситета.
Расчет производится по формуле
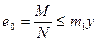 , (32)
, (32)
где М - момент от расчетной поперечной нагрузки и внецентренного приложения нормальной силы;
N - нормальная сила от расчетного собственного веса элемента, вычисленного с учетом коэффициента перегрузки 0,9;
m1 - коэффициент, принимаемый для стен в стадии их возведения и свободно стоящих стен равным m1 =0,9, а для сооружений - по специальным указаниям;
у - расстояние от центра тяжести элемента до края сечения в сторону эксцентриситета.
Пример 1. Расчет участка стены таврового сечения на внецентренное сжатие (эксцентриситет в сторону ребра).
К тавровому сечению простенка приложена расчетная продольная сила N = 850 кН (85 тс) и расчетный момент, направленный в сторону ребра М = 102 кН×м (10,2 тс×м).
Размеры сечения приведены на черт. 6. Высота этажа Н =5 м. Кладка выполнена из глиняного кирпича пластического прессования марки 100 на растворе марки 50, расчетное сопротивление кладки R= 1,5МПа (15 кгс/см2).
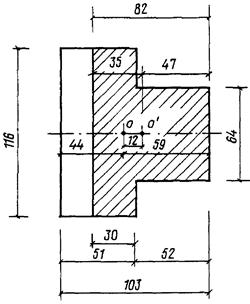
Черт. 6. Поперечное тавровое сечение
Перекрытие сборное железобетонное, заделанное на опорах в кладку стены, толщина перекрытия Hf = 0,22м.
Здание жесткой конструктивной схемы (перекрытие является неподвижной горизонтальной опорой стены).
Найти расчетную несущую способность Ncc.
Эксцентриситет
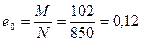 м.
м.
Расчет производим по указаниям п. [4.7, формула (13)]:
N£mgj1RAcw.
Определяем геометрические характеристики сечения.
Площадь сечения
А = 0,51×1,16+0,52×0,64= 0,924м2.
Определяем расстояние центра тяжести сечения от края полки по графику прил. 5:
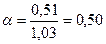 ;
; 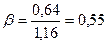 ;
;
x = 0,43; z0 = 0,43×1,03 = 0,44 м.
Расстояние от центра тяжести сечения до его края в сторону эксцентриситета
у =h - z0 = 1,03 - 0,44 = 0,59 м.
Момент инерции сечения относительно его центра тяжести определяем по графику прил. 5:
I = 0,0605×1,16×1,033 =7,67×10-2 м4.
Радиус инерции сечения
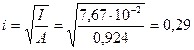 м
м
Так как i > 0,087 м, то согласно п. [4.7] принимается mg = 1.
Определяем значение коэффициента продольного изгиба j для всего сечения.
Расчетная высота простенка l0 при условиях, указанных в задании в соответствии с п. [4.3, примеч. 1], принимается равной
l0 = 0,9H = 0,9 (5 - 0,22) = 4,3 м.
Гибкость простенка определяется по формуле
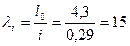 .
.
Упругая характеристика кладки из глиняного кирпича пластического прессования, выполненной на растворе марки 50,
a = 1000 по табл. [15].
Коэффициент продольного изгиба принимаем по табл.[18]
j=0,99.
Определяем площадь сжатой части сечения.
Для определения размеров этой площади применяем формулу (2) прил. 6:
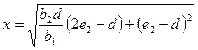 ,
,
где х - расстояние от точки приложения силы до края полки сжатой части сечения.
Точка приложения силы совпадает с центром тяжести сжатой части сечения
b1 = 1,16м; b2 = 0,64м; d= 0,52м;
е2 = у – е0 = 0,59 - 0,12 = 0,47 м;
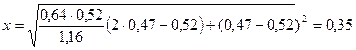 м.
м.
Высота сжатой части сечения
hс = е2 + х = 0,47 + 0,35 = 0,82 м.
Площадь сжатой части сечения
Ас = 0,64×0,32 + 0,30×0,26×2 = 0,681 м2.
Определяем момент инерции сжатой части сечения относительно его центра тяжести по графику прил. 5:
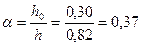 ;
;
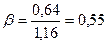 ; h=0,061;
; h=0,061;
Ic=hbh3=0,061×1,16×0,823=3,9×10-2 м4.
Радиус инерции сжатой части сечения
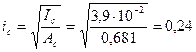 м
м
Коэффициент продольного изгиба для сжатой части сечения при 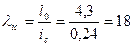 ; по табл. [18] jc=0,97
; по табл. [18] jc=0,97
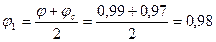 .
.
Так как радиус инерции сечения i = 0,290 > 0,087 м, то коэффициент mg в формуле [13] принимаем равным единице. Коэффициент w принимаем по табл. [19]:
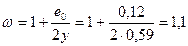 .
.
Расчетная несущая способность простенка Ncc:
Ncc = mgj1RAcw = 0,98×1,5×0,681×1,1 103 = 1100 кН > 850 кН (110 тc > 85 тc).
Расчетная продольная сила N меньше расчетной несущей способности Ncc, следовательно, простенок удовлетворяет требованиям прочности.
Относительный эксцентриситет
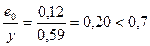 ,
,
поэтому, согласно п. [4.8], расчет по раскрытию трещин не производится.
Пример 2. Расчет участка стены таврового сечения на внецентренное сжатие (эксцентриситет в сторону полки).
К тавровому сечению простенка приложена продольная сила с эксцентриситетом e0 = 0,16 м в сторону полки. Размеры простенка и все остальные данные см. на черт. 7.
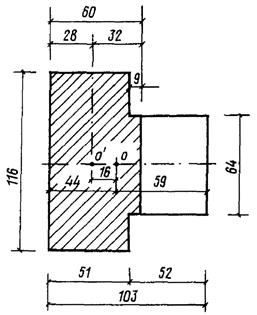
Черт. 7. Поперечное тавровое сечение
Найти расчетную несущую способность Ncc.
Расчет производим по формуле [13] п. [4.7]:
N £ mgj1RAcw.
Следующие величины, не зависящие от эксцентриситета, вычисленные в примере 1, остаются без изменений:
z0 = 0,44м; a = 1000; l0 = 4,30м;
mg = 1; j = 0,99; R = 1,5 МПа (15 кгс/см2);
А = 0,924 м2; I = 7,67 10-2 м4.
Расстояние от центра тяжести сечения до края сечения в сторону эксцентриситета
у = z0 = 0,44м.
Нормальная сила приложена на расстоянии
e1 = z0 – е0 = 0,44-0,16 = 0,28м
от наружного края полки сечения.
Определяем площадь сжатой части сечения.
Для определения размеров этой площади применяем формулу (1) прил.6:
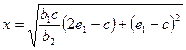 ,
,
где х - расстояние от точки приложения силы до края ребра расчетной части сечения;
b1 = 1,16м; b2 = 0,64м; с= 0,51м; e1 = 0,28 м;
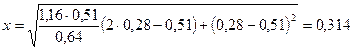 м
м
Размеры расчетной сжатой части сечения показаны на черт. 7.
Площадь сжатой части сечения
Ас = 1,16×0,51 + 0,09×0,64 = 0,649 м2.
Определяем момент инерции сжатой зоны сечения относительно его центра тяжести по графику прил. 5:
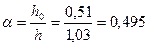 ;
;
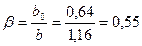 ; h=0,060;
; h=0,060;
Ic=hbh3;
Ic=0,060×1,16×0,603=1,5.10-2 м4
Радиус инерции сжатой части сечения
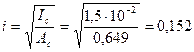 м.
м.
Коэффициент продольного изгиба для сжатой части сечения при гибкости
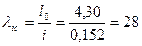 .
.
Принимаем по табл. [18] jс = 0,92 и определяем
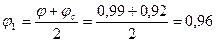 .
.
Коэффициент w принимаем по табл. [19].
Так как 2у = 2×0,44 = 0,88 < h = 1,03, то коэффициент w равен
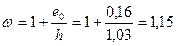 .
.
Расчетная несущая способность сечения определяется по формуле [ 13]:
Nсс = mgj1RAcw = = 0,96×1,5×103×0,649×1,15 = 1080 кН > 850 кН (108 тс > 85 тс).
Расчетная продольная сила N меньше расчетной несущей способности Nсс следовательно, простенок удовлетворяет требованиям прочности.
Относительный эксцентриситет
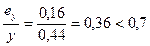 .
.
Поэтому согласно п. [4.8] расчет по раскрытию трещин не производится.
Пример 3. Расчет участка стены таврового сечения по несущей способности и по раскрытию трещин.
К тавровому сечению простенка приложена продольная сила с эксцентриситетом е0=0,45 м в сторону ребра.
Размеры простенка и все остальные данные см. на черт.8.
Найти расчетную несущую способность Nсс. Следующие величины, не зависящие от эксцентриситета, вычисленные в примере 1, остаются без изменения:
z0 = 0,44м; a = 1000; l0 = 4,30м;
mg = 1; j = 0,99; R = 1,5 МПа (15 кгс/см2);
А = 0,924 м2; I = 7,67 10-2 м4.
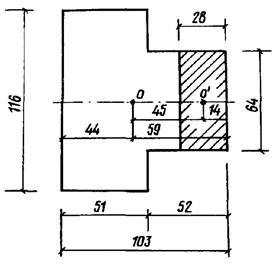
Черт. 8. Поперечное тавровое сечение
Расстояние от центра тяжести до края сечения в сторону эксцентриситета
у = h – z0 = 1,03 -0,44 = 0,59 м;
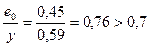 ,
,
следовательно, простенок должен быть рассчитан не только по несущей способности, но и по раскрытию трещин в растянутой зоне сечения.
А. Вычисление Nсс по несущей способности.
Расчет производим по формуле [13]:
Nсс = mgj1RAcw.
Расстояние s от точки приложения силы до края ребра сечения равно
s = у – е0 = 0,59 - 0,45 = 0,14 м < 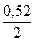 ,
,
т. е. меньше половины высоты ребра. Поэтому сжатая часть сечения прямоугольная и высота ее определяется по формуле
hc = 2s = 2×0,14 = 0,28 м.
Расчетная сжатая часть сечения показана на черт.8:
Ас = 0,28×0,64 = 0,179м2.
Коэффициент продольного изгиба для сжатой части сечения при гибкости
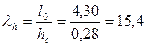
по табл. [18] jc = 0,76:
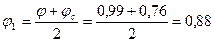 .
.
Коэффициент w принимаем по табл. [19]:
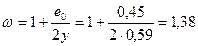 .
.
Расчетная несущая способность простенка
Ncc = 0,88×1,5×103×0,179×1,38 = 326 кН (32,6 тc).
Б. Определение Ncc no раскрытию трещин в растянутой зоне сечения производим по формуле [33] п. [5.3]:
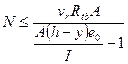 .
.
Согласно табл. [24] при предполагаемом сроке службы конструкции 50 лет vr = 2,0.
По табл. [10] принимаем Rtb = 0,12 МПа и определяем
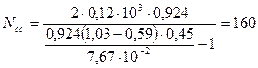 кН (16 тс).
кН (16 тс).
Таким образом, предельная нагрузка на простенок определяется в данном случае расчетом по раскрытию трещин в растянутой зоне сечения, а не расчетом по несущей способности.
Пример 4. Расчет несущей способности участка несущей стены здания с жесткой конструктивной схемой.
К участку стены прямоугольного сечения приложена расчетная продольная сила N = 165 кН (16,5 тс), от длительных нагрузок Ng = 150кН (15 тс), кратковременных Nst = 15 кН (1,5 тc). Размер сечения 0,24´1,00м, высота этажа 3 м, нижние и верхние опоры стены - шарнирные, неподвижные. Стена запроектирована из газобетонных блоков двухрядной разрезки, смонтированных на растворе проектной марки М50; газобетон вида А плотностью 8 кН/м3 (800 кгс/м3) проектной марки по прочности М50. Расчетная установившаяся влажность газобетона W = 10 % (по массе).
Требуется проверить несущую способность элемента стены в середине высоты этажа при возведении здания в летних условиях.
В соответствии с п. [4.9] для несущих стен толщиной 0,24 м следует учитывать случайный эксцентриситет еv = 0,02 м. Следовательно, продольная сила будет действовать с эксцентриситетом e0 = e0g = еv = 0,02 м. Расчет производим по формуле [13]:
N£ mgj1RAcw.
Находим геометрические характеристики сечения. Площадь сечения элемента
А = 0,24×1,0 = 0,24м2.
Площадь сжатой части сечения по формуле [14]:
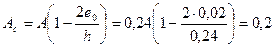 м2.
м2.
Расстояние от центра тяжести сечения до края сечения в сторону эксцентриситета
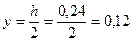 м.
м.
Расчетное сопротивление сжатию кладки R по табл. [4] с учетом коэффициента условий работы gс = 0,8, см. п. [3.11], равно
R = 1,5×1,1×0,8 = 1,32 МПа (13,2 кгс/см2).
Расчетная длина элемента согласно черт. [4, а], п. [4.3] равна
l0 = H = 3 м.
Гибкость элемента равна
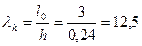 .
.
Упругая характеристика кладки a, принимаемая по табл. [15], равна
a = 750.
Коэффициент продольного изгиба определяем по табл. [18]:
j = 0,775.
Гибкость сжатой части сечения
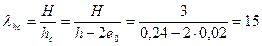 .
.
Коэффициент продольного изгиба сжатой части сечения по табл. [18]:
jc = 0,705.
По формуле [15] определяем коэффициент j1:
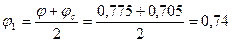 .
.
Коэффициент w для ячеистого бетона принимается по табл. [19] равным 1,0.
Коэффициент h при lhc = 15 по табл. [20] принимаем равным 0,115.
Коэффициент mg по формуле [16] равен
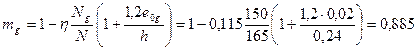 .
.
Расчетная несущая способность участка стены Ncc равна
Nсс = mgj1RAcw = 0,885×0,74×1,32×103×0,2×1 = 172,9 кН (17,29 тc).
Расчетная продольная сила N меньше Nсс:
N = 165 кН < Ncc = 172,9 кН.
Следовательно, стена удовлетворяет требованиям по прочности. Эксцентриситет е0=0,02 м, что меньше 0,7 у = 0,7×0,12 = 0,084 м, поэтому в соответствии с п. [4.8] не следует производить расчет по раскрытию трещин.
Пример 5. Расчет участка внутренней несущей стены здания с жесткой конструктивной схемой на внецентренное сжатие.
К участку стены прямоугольного сечения приложена расчетная продольная сила N=200 кН (20 тc) от длительных нагрузок Ng = 180 кН (18 тc), кратковременных Nst = 2кН (2 тc) и расчетный момент М = 3,9 кН×м (0,39 тc×м). Размер сечения 0,24´1,00 м, высота этажа H = 3 м, нижние и верхние опоры стены - шарнирные неподвижные. Стена запроектирована из газобетонных блоков двухрядной разрезки, смонтированных на растворе проектной марки М50; газобетон вида А плотностью 10 кН/м (1000 кгс/м3), проектной марки по прочности М100. Расчетная установившаяся влажность газобетона W = 10% (по массе).
Требуется проверить несущую способность элемента стены в середине высоты этажа при возведении здания в летних условиях. Эксцентриситет от расчетной продольной силы равен
e0 = M/N = 3,9:200 = 0,0195 м.
Случайный эксцентриситет в соответствии с п. [4.9] для несущих стен толщиной 0,24 м равен ev = 0,02 м. Эксцентриситет от действия длительных нагрузок e0g1 = M/Ng=3,9:180 = 0,0217 м.
Расчетный эксцентриситет принимаем равным:
от расчетной продольной силы с учетом случайного эксцентриситета
e0=e01+ev = 0,0195+0,02 = 0,0395м @ 0,04м;
от действия длительных нагрузок с учетом случайного эксцентриситета
e0g=e0g1+ev = 0,0217 + 0,02 = 0,0417 м @ 0,042 м.
Расчет производим по формуле [13]
N£ mgj1RAcw.
Находим геометрические характеристики сечения. Площадь сечения элемента
А = 0,24×1,0 = 0,24м2.
Площадь сжатой части сечения по формуле [14]
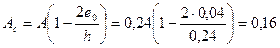 м2.
м2.
Расстояние от центра тяжести сечения до края сечения в сторону эксцентриситета
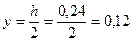 м.
м.
Расчетное сопротивление сжатию кладки R по табл. [4] с учетом коэффициента условий работы gс = 0,8 п. [3.11] равно
R = 2,7×1,1×0,8 = 2,376 МПа (23,76 кгс/см2).
Расчетная длина элемента l0 согласно черт. [4, a], п. [4.3]
l0 = H = 3 м.
Гибкость элемента по формуле [12]
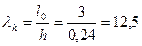 .
.
Упругая характеристика a по табл. [15] равна 750.
Гибкость сжатой части сечения lhc равна
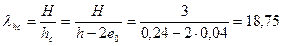 .
.
Коэффициент продольного изгиба сжатой части сечения jc по табл. [18] равен 0,611.
По формуле [15] коэффициент 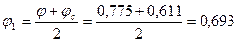 .
.
Коэффициент w для ячеистого бетона принимаем по табл. [19] равным 1,0.
Коэффициент h при lhc = 18,75 по табл. [20] принимаем равным 0,209.
Коэффициент mg, по формуле [16] равен
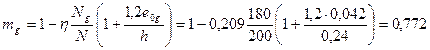 .
.
Расчетная несущая способность элемента стены
Ncc = mgj1RAcw = 0,772×0,693×2,376×103×0,16×1 = 203,4 кН (20,34 тc).
Расчетная продольная сила N меньше расчетной несущей способности Ncc:
N = 200 кН < Ncc = 203,4 кН.
Следовательно, стена удовлетворяет требованиям по прочности. Относительный эксцентриситет e0/у = 0,04:0,12 = 0,33 < 0,7, поэтому в соответствии с п. [4.8] расчет по раскрытию трещин производить не требуется.
Пример 6. Расчет кладки на смятие под опорами свободно лежащей однопролетной стальной двутавровой балки чердачного перекрытия.
Балка № 20 с моментом инерции поперечного сечения I = 1840×10-8 м4 длиной 6,4 м с пролетом (в свету) 6 м, шириной полки b = 0,1 м и длинами опорных концов a1 = 0,2 м с каждой стороны. Балка нагружена равномерно распределенной нагрузкой q = 5 кН/м (500 кгс/м), включая ее собственный вес. Балки чердачного перекрытия опираются на кирпичные стены толщиной 0,51 м, выполненные из кирпича марки 100 на растворе марки 50. Расчетное сопротивление кладки 1,5 МПа. Расстояние между балками 1,5 м. Опорная реакция балки Q = 15 кН (1,5 тc).
Расчет кладки на смятие под опорами балки производим по п. [4.15].
Полезную длину опоры a0 определяем по формуле (13):
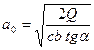 .
.
Коэффициент постели с при смятии кладки под концом балки при затвердевшей кладке определяется по формуле
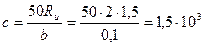 МН/м3 (1,5×105 тс/м3)
МН/м3 (1,5×105 тс/м3)
При равномерно распределенной нагрузке тангенс угла наклона оси балки в середине опорного конца определяется по формуле
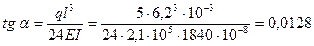 ;
;
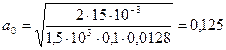 м <0,2 м.
м <0,2 м.
Расчет кладки на смятие под опорами балки производится по формуле [17] п. [4.13]:
Nс £ ydRсAc.
Так как полезная длина опоры балки a0 меньше ее полной длины a1, то эпюра распределения напряжений принимается по треугольнику с коэффициентом полноты y=0,5; d=1,5-0,5y=1,25. По п. [4.14] расчетное сопротивление кладки при смятии Rc=xR. Расчетная площадь сечения А принимается по п. [4.16в]:
А = (0,1+0,51×2)0,125 = 0,14м2.
Площадь смятия Аc = 0,1×0,125 = 0,0125 м2.
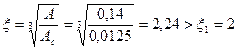 .
.
Расчетное сопротивление кладки на смятие Rc = xR.
Rc = 1,5×2 = 3 МПа.
Расчетная несущая способность затвердевшей кладки при смятии
Nсc £ ydRсAc=0,5×1,25×3×0,0125×103=23,4>Q=15 кН (2,34 тс>1,5 тс).
Расчетная нагрузка на стену при смятии меньше расчетной несущей способности кладки, следовательно, затвердевшая кладка под опорой балки удовлетворяет требования прочности.
Определяем расчетную несущую способность свежей кладки при смятии.
Коэффициент постели с1 для свежей кладки при прочности раствора 0,2 МПа и расчетном сопротивлении кладки 0,8 МПа определяется по формуле
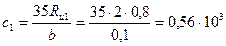 мН/м3 (0,56×105 тс/м3);
мН/м3 (0,56×105 тс/м3);
tg a=0,0128;
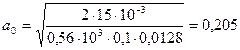 м > 0,2 м.
м > 0,2 м.
Краевые напряжения при эпюре в виде трапеции определяются по формулам:
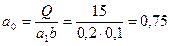 МПа;
МПа;
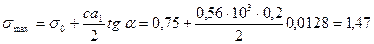 МПа
МПа
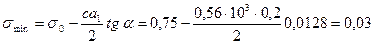 МПа
МПа
Коэффициент полноты эпюры давления при эпюре напряжений под опорой балки в виде трапеции определяется по формуле
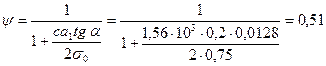 ;
;
d = 1,5-0,5×0,51 = 1,245.
Расчетная площадь сечения А = (0,1+0,51×2)0,2= 0,224м2.
Площадь смятия Aс = 0,1×0,2 = 0,02 м2.
Коэффициент определяем по формуле [19]:
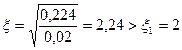 ;
;
Rc = 0,8×2 = 1,6 МПа.
Расчетная несущая способность свежей кладки при смятии
Ncc = 0,51×1,245×1,6×103×0,02 = 20,3 кН > Q = 15 кН (2,03 тс > 1,5 тс).
Расчетная нагрузка на стену при смятии меньше расчетной несущей способности кладки, следовательно, свежая кладка под опорой балки также удовлетворяет требованиям прочности.
Пример 7. Расчет на смятие кладки под опорным участком балки покрытия.
Рассчитать и сконструировать опоры для двускатных балок покрытия над одноэтажным промышленным зданием пролетом 15 м. Балки опираются на наружные стены с пилястрами, шаг - 6м. Стены толщиной 0,38 м возводятся из кирпича марки 75 на растворе марки 50, сечение пилястр 0,39´0,51 м, см. черт. 9 и 10. Учитывая, что монтаж покрытия может быть произведен через 7-10 сут после возведения кладки и при температуре, равной 10°С, принимаем прочность раствора с коэффициентом 0,5 (см. табл. 1), т. е. марки 25.
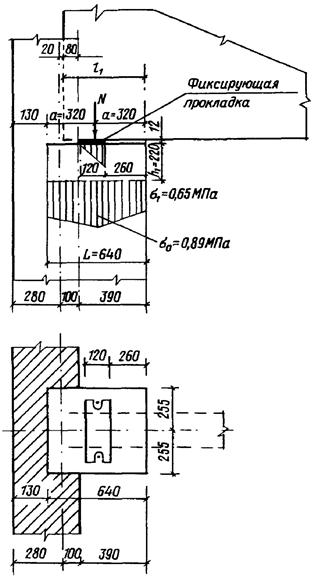
Черт. 9. Схема узла опирания балки на стену под опорной
пятой в направления оси балки
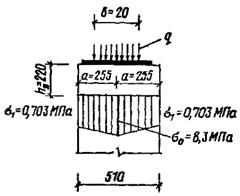
Черт. 10. Распределение напряжений в кладке под опорной плитой
в поперечном направлении
Вертикальная расчетная нагрузка на опору N = 250 кН (25 тc). Балки опираются на кладку через железобетонные распределительные плиты, расположенные по всему сечению пилястр и на части сечения наружной стены.
Принимаем предварительные размеры опорной плиты: ширину, равную ширине пилястры, длину 0,64 м и высоту 0,22 м. Армирование плиты производим в соответствии с требованиями п. 4.14.
Балка на опорную плиту опирается через фиксирующую прокладку, размеры которой определяются из условия местного смятия бетона плиты.
Наиболее благоприятное распределение напряжений под опорной плитой будет при размещении фиксирующей прокладки по центральным осям опорной плиты. В этом случае коэффициент неравномерности распределения напряжений под опорной плитой определяется в основном жесткостью этой плиты.
Напряжения вдоль оси опорной плиты, перпендикулярной оси стены, определяем по формулам табл. 6 поз. 2 (см. черт. 9):
а = 0,32м; d = 0,51 м.
Модуль упругости опорной плиты
Е = 0,85Eb = 0,85×265×102 = 225×102 МПа.
Момент инерции распределительной плиты
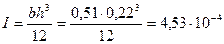 м4.
м4.
Модуль упругости кладки
Е = 0,5 Е0 = 0,5 aRu = 0,5×1000×2,2 = 1100 МПа.
Высота распределительной плиты
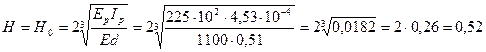 м.
м.
По табл. 6 поз. 2 принимаем
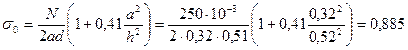 МПа (8,8 кгс/см2);
МПа (8,8 кгс/см2);
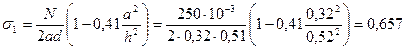 МПа (6,50 кгс/см2).
МПа (6,50 кгс/см2).
Определяем коэффициент полноты эпюры давления y1, учитывая, что объем эпюры давления равен N
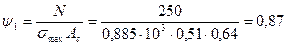 .
.
Напряжения вдоль оси опорной плиты, параллельной оси стены, определяем по табл. 6, поз. 8 (см. черт. 10):
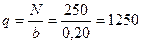 кН/м;
кН/м;
b=0,20 м; d1=0,64 м; а=0,255 м.
По формуле (26) находим
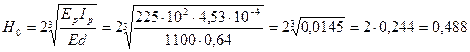 м;
м;
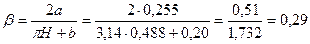 ;
;
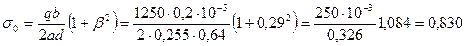 МПа (8,30 кгс/см2);
МПа (8,30 кгс/см2);
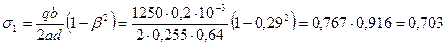 МПа (7,03 кгс/см2);
МПа (7,03 кгс/см2);
s1=0,703 МПа<R=1,1 МПа (11 кгс/см2)
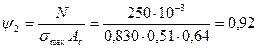 ;
;
y=y1y2=0,87×0,92=0,80.
Расчетную несущую способность опоры определяем в соответствии с формулой [17]:
Nсc=ydRсAc;
d=1,5-0,5y=1,5-0,5×0,80=1,1;
yd=0,80×1,1=0,88;
Rc=xR=1×1,1 МПа;
Ac = 0,51×0,64=0,326 м2;
Ncc=0,88×1,1×0,326×103=316 кН>N=250 кН(31,6 тс>25 тc).
Кирпичную кладку под опорной плитой в соответствия с пп. 4.14 и 4.23 армировать не требуется, так как N<0,8Nc и v>0,8.
5. РАСЧЕТ И КОНСТРУИРОВАНИЕ АРМИРОВАННЫХ,
КОМПЛЕКСНЫХ И УСИЛЕННЫХ ОБОЙМАМИ
КАМЕННЫХ КОНСТРУКЦИЙ
 2015-04-01
2015-04-01 1219
1219








