Основные понятия. Пусть дана последовательность чисел (вещественных или комплексных)

Пусть дана последовательность чисел (вещественных или комплексных)

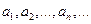
Определение. Выражение 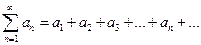называют числовым рядом, или просто рядом, а сами числа 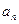- членами ряда.

Числовой ряд будем обозначать .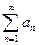

Ряд считается заданным, если известен общий член ряда 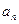, выраженный как функция его номера n: .

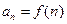Определение. Сумма первых n членов ряда 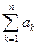называется n-й частичной суммой ряда и обозначается 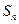, т.е.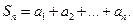

Рассмотрим частичные суммы:

,…,

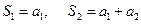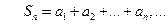
Определение. Если последовательность 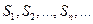имеет конечный предел: 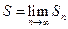, то говорят, что ряд 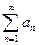сходится. В этом случае, предел 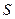называют суммой ряда и пишут: .

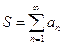Ряд 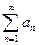расходится, если последовательность 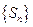не имеет предела или он равен 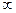. Если 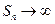, то говорят, что сумма ряда равна 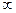, и пишут: .

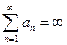Пример. Показать, что числовой ряд 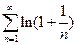расходится.

Решение. Запишем n -ю частичную сумму ряда. Имеем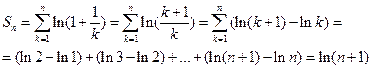

Тогда при 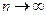имеем 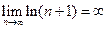. Следовательно, ряд расходится, и считается,что его сумма равна .

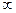Пример. Показать, что ряд 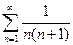сходится.

Решение. Частичные суммы ряда имеют вид: 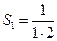, , 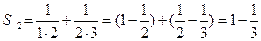…, 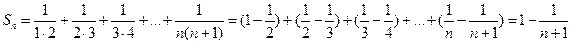. Вычислим сумму ряда: 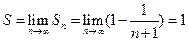, т.е. ряд сходится, и его сумма равна 1.

Пример. Исследовать на сходимость ряд, члены которого образуют геометрическую прогрессию: = .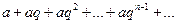

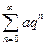
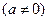Решение. Сумма первых n членов прогрессии вычисляется по формуле 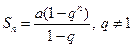. Найдем предел этой суммы: .

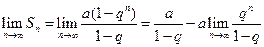В зависимости от величины q имеем:

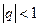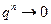1) если , то при 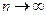. Поэтому 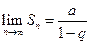, ряд сходится, его сумма равна ;

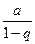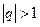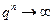2) если , то при 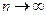. Поэтому 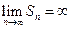, ряд расходится;

3) если 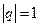, то при 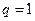ряд принимает вид ,

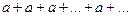для него 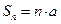и 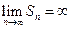, т.е. он расходится;

при 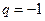ряд принимает вид 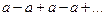, в этом случае 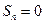при четном n и 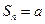при нечетном n. Следовательно, 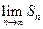не существует, ряд расходится.

Таким образом, ряд сходится при 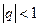и расходится при 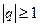. Такой ряд будем называть рядом геометрической прогрессии.