Мы уже отмечали, что условия, при выполнении которых функция 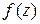 является аналитической, достаточно жесткие. Это и обуславливает справедливость следующей теоремы.
является аналитической, достаточно жесткие. Это и обуславливает справедливость следующей теоремы.
Теорема 2 (Теорема Коши). Если 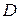 - односвязная область комплексной плоскости и
- односвязная область комплексной плоскости и 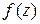 - однозначная аналитическая в этой области функция, то для любой замкнутой спрямляемой кривой
- однозначная аналитическая в этой области функция, то для любой замкнутой спрямляемой кривой 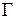 , лежащей в области
, лежащей в области 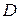 , интеграл от
, интеграл от 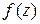 вдоль
вдоль 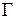 равен нулю:
равен нулю: 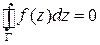 .
.
Отметим, что теорема Коши остается справедливой и для многосвязной области.
Из теоремы 2 вытекает, что интегралы от аналитической функции вдоль любых двух кривых 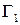 и
и 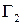 с общим началом
с общим началом 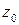 и концом
и концом 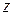 имеют равные значения.
имеют равные значения.
В самом деле, кривая 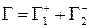 является замкнутой, и, следовательно,
является замкнутой, и, следовательно,
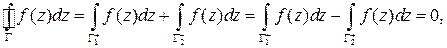 откуда
откуда
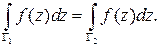
Это означает, что интеграл от функции 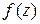 , аналитической в односвязной области
, аналитической в односвязной области 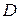 , не зависит от кривой
, не зависит от кривой 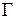 (от пути интегрирования), а зависит только от начальной и конечной точек этой кривой. Поэтому для интеграла вдоль произвольной спрямляемой кривой
(от пути интегрирования), а зависит только от начальной и конечной точек этой кривой. Поэтому для интеграла вдоль произвольной спрямляемой кривой 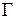 , соединяющей точки
, соединяющей точки 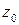 и
и 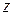 , можно пользоваться обозначением
, можно пользоваться обозначением 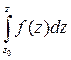 .
.
Рассмотрим интеграл от аналитической функции, если конечная точка – переменная, т.е. 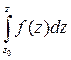 есть некоторая функция от верхнего предела:
есть некоторая функция от верхнего предела:
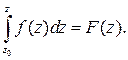
Можно показать, что 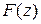 - аналитическая функция, и что ее производная равна
- аналитическая функция, и что ее производная равна 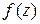 . Таким образом, интеграл
. Таким образом, интеграл 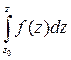 является первообразной для подынтегральной функции (определение первообразной аналитической функции аналогично определению первообразной функции действительной переменной).
является первообразной для подынтегральной функции (определение первообразной аналитической функции аналогично определению первообразной функции действительной переменной).
И это позволяет сделать вывод о справедливости формулы Ньютона-Лейбница:
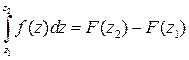 ,
,
здесь 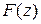 - одна из первообразных функции
- одна из первообразных функции 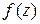 , (
, (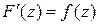 ).
).
Этот результат позволяет сводить вычисление интеграла от аналитической функции 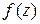 к отысканию какой-либо первообразной функции и, следовательно, использовать известные формулы и методы интегрирования функций действительной переменной. В частности, если
к отысканию какой-либо первообразной функции и, следовательно, использовать известные формулы и методы интегрирования функций действительной переменной. В частности, если 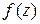 и
и 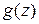 аналитические функции, то будет справедлива формула интегрирования по частям:
аналитические функции, то будет справедлива формула интегрирования по частям:
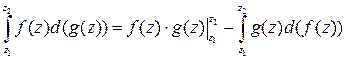 .
.
Пример. Вычислить интеграл 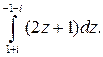
Решение. Подынтегральная функция является аналитической на всей комплексной плоскости, поэтому для нее существует первообразная. Воспользуемся формулой Ньютона-Лейбница:
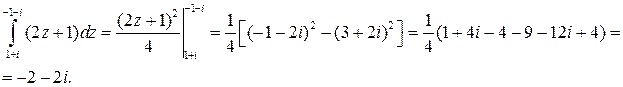
Пример. Вычислить интеграл 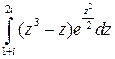 .
.
Решение. Подынтегральная функция является аналитической, поэтому воспользуемся формулой интегрирования по частям:
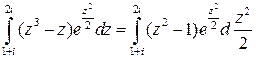 =
= 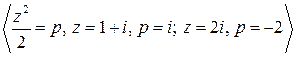 =
=
= 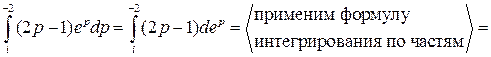
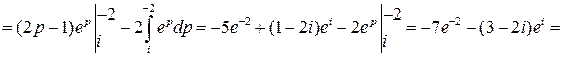
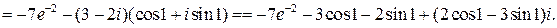
Аналитические функции комплексного переменного обладают следующим замечательным свойством:
Теорема 3. (Интегральная формула Коши) Если 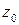 - внутренняя точка односвязной области
- внутренняя точка односвязной области 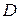 , ограниченной замкнутым контуром
, ограниченной замкнутым контуром 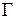 ,
, 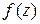 - аналитическая в замкнутой области
- аналитическая в замкнутой области 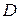 функция, то справедлива формула:
функция, то справедлива формула:
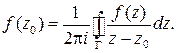
Иными словами, если мы знаем значение аналитической функции на границе односвязной области, то мы можем найти значение этой функции в любой внутренней точке области.
Более того, справедлива следующая теорема.
Теорема 4. Если однозначная функция комплексного переменного 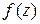 имеет всюду в области
имеет всюду в области 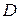 первую производную, то она имеет в этой области и все производные высших порядков, которые могут быть найдены по формуле:
первую производную, то она имеет в этой области и все производные высших порядков, которые могут быть найдены по формуле:
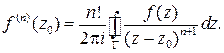
Интегральную формулу Коши и формулу для производных высших порядков можно использовать для вычисления интегралов по замкнутому контуру.
Пример. Вычислить интеграл 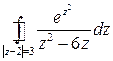 .
.
Решение. Рассмотрим подынтегральную функцию 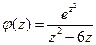 . Аналитичность этой функции нарушается в точках:
. Аналитичность этой функции нарушается в точках: 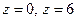 (точки, в которых знаменатель равен 0). Контур, по которому вычисляется интеграл:
(точки, в которых знаменатель равен 0). Контур, по которому вычисляется интеграл: 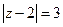 , есть окружность с центром в точке
, есть окружность с центром в точке 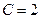 и радиусом 3. Внутри этого контура лежит точка
и радиусом 3. Внутри этого контура лежит точка 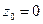 , поэтому внутри контура подынтегральная функция не является аналитической. Запишем эту функцию в виде:
, поэтому внутри контура подынтегральная функция не является аналитической. Запишем эту функцию в виде: 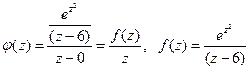 . Тогда функция
. Тогда функция 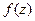 является аналитической внутри замкнутого контура. Воспользуемся интегральной формулой Коши:
является аналитической внутри замкнутого контура. Воспользуемся интегральной формулой Коши:
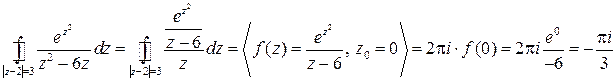 .
.
Пример. Вычислить интеграл 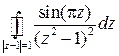 .
.
Решение. Аналитичность подынтегральной функции нарушается в точках 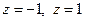 . Внутри контура есть только одна из них:
. Внутри контура есть только одна из них: 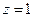 . Преобразуем подынтегральную функцию к виду:
. Преобразуем подынтегральную функцию к виду:
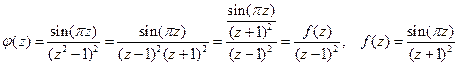 .
.
Функция 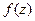 - аналитическая внутри контура, поэтому можно применить теорему 4 (в данном случае
- аналитическая внутри контура, поэтому можно применить теорему 4 (в данном случае 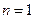 ):
):
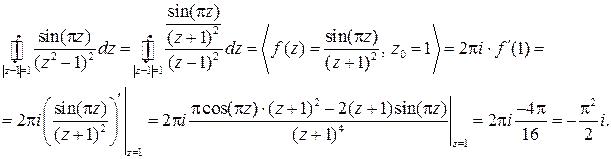
 2015-04-01
2015-04-01 6821
6821
