Пусть в вероятностной модели 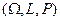 пространство элементарных исходов
пространство элементарных исходов 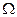 - бесконечное непрерывное множество, для которого определена мера. Роль меры множества играют: длина для линейных множеств, площадь для плоских множеств, объем для пространственных множеств. Будем обозначать меру множества А – mes(A).
- бесконечное непрерывное множество, для которого определена мера. Роль меры множества играют: длина для линейных множеств, площадь для плоских множеств, объем для пространственных множеств. Будем обозначать меру множества А – mes(A).
Пусть на множестве 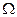 определена функция
определена функция 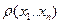 ,
, 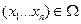 , удовлетворяющая условию
, удовлетворяющая условию 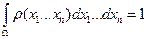 .
.
Если А - некоторое событие, связанное с этой моделью, т.е. 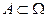 , тогда вероятность этого события определяется по формуле:
, тогда вероятность этого события определяется по формуле: 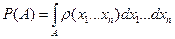 . Эта числовая функция удовлетворяет всем аксиомам вероятности.
. Эта числовая функция удовлетворяет всем аксиомам вероятности.
В частном случае, когда 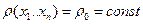 , из условия:
, из условия: 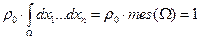 , получим, что
, получим, что 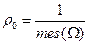 . Тогда для вероятности случайного события имеем:
. Тогда для вероятности случайного события имеем: 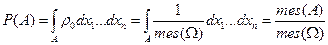 .
.
Определение. Вероятность события A, определяемая формулой: 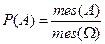 называется геометрической вероятностью.
называется геометрической вероятностью.
Пример. Эксперимент состоит в радиолокационном наблюдении воздушной цели. Наблюдаемый результат – положение светящегося пятна на экране индикатора цели, имеющего форму круга, радиуса 10 см. Найти вероятность следующих событий: A={цель находится в первом квадранте} B={цель находится в круге радиуса 5 см с центром в центре экрана}.
Решение. Все события связаны с регистрацией положения светящегося пятна на экране. Элементарным исходом являются координаты точки на плоскости в декартовой системе координат, связанной с центром экрана. Таким образом, пространство элементарных исходов бесконечно, непрерывно и может быть записано в виде: 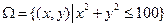 . Мера этого множества – его площадь:
. Мера этого множества – его площадь: 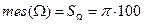 . Подмножества, соответствующие указанным событиям:
. Подмножества, соответствующие указанным событиям:
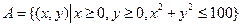 ,
, 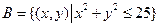 .
.
По формуле геометрической вероятности имеем: 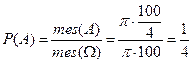 ,
, 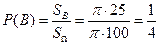 .
.
 2015-04-01
2015-04-01 2883
2883








