2015-04-01
334
Отношение R на М называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.
Равенство – это минимальное отношение эквивалентности в том смысле, что при удалении любой пары из Е (т. е. любой единицы на диагонали матрицы Е) оно перестает быть рефлексивным и, следовательно, уже не является эквивалентным.
Пусть на множестве М задано отношение эквивалентности R. Осуществим построение классов эквивалентности, на которые разбивается множество М этим отношением.
Выберем элемент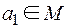 
и образуем класс (подмножество М) 
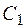, состоящий из 
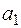и всех элементов, эквивалентных 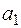; затем выберем элемент 
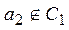, и образуем класс 
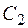, состоящий из 
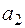и всех элементов, эквивалентных 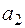и т. д. Получится система классов 
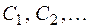(возможно бесконечная) такая, что любой элемент из М входит хотя бы в один класс, т. е. 
.
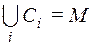Эта система обладает свойствами:
1) она образует разбиение, т. е. классы попарно не пересекаются;
2) любые два элемента из одного класса эквивалентны;
3) любые два элемента из разных классов неэквивалентны.
Мощность системы классов эквивалентности называется индексом разбиения.
С другой стороны, любое разбиение М на классы определяет некоторое отношение эквивалентности.
