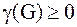Теорема 5

. Причем, если

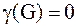, то граф не имеет циклов, то есть является деревом или лесом;

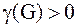, то граф имеет ровно 1 цикл.

Число внутренней устойчивости графа G обозначается 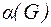– это максимальное число несмежных вершин графа.

Множеством внешней устойчивости графа G (внешне устойчивым множеством)называется любое множество вершин Q такое, что из каждой вершины множества 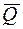хотя бы одна дуга ведет в вершину множества Q. Если граф неориентированный, то число внешней устойчивости ищется для канонически соответствующего ориентированного графа.

Число внешней устойчивости графа G обозначается 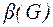– это мощность минимального внешне устойчивого множества.

Сетью называется любой частично-ориентированный граф S, некоторые вершины которого помечены.

Некоторые помеченные вершины называются входными полюсами, другие – выходными полюсами. Непомеченные вершины называются внутренними. Простая цепь, связывающая входной и выходной полюс будет называться цепью.

Если сеть содержит k входных и n выходных полюсов, то она называется ( k, n)- полюсником.

Двухполюсной сетью называется сеть, являющаяся (1, 1)-полюсником.

Пусть дана частично ориентированная двухполюсная сеть. Пусть для каждого ребра сети определена пропускная способность ребра .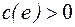

Потоком в сети называется пара объектов 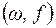, где 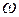– некоторая ориентация неориентированных ребер сети, f = f(e), функция значения потока на ребре е, которая удовлетворяет следующим условиям:

1. ограничение:

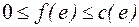
2. для каждой внутренней вершины выполняется закон Киргоффа:

,

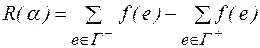где 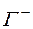– множество ребер выходящих из вершины ,

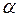где 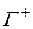– множество ребер входящих в вершину .

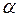Если 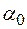– входной полюс сети, а 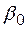– выходной полюс, то

.

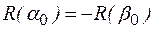Величиной потока в сети назовем число 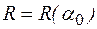. Очевидно, что величина потока в сети зависит и от ориентации ребер 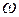, и от задания функции f(e), то есть является величиной переменной.

Сечением в сети называется совокупность ребер, при удалении которых сеть становится несвязной. Сечение называется простым, если при удалении из него хотя бы одного ребра, оно перестает быть сечением.

Утверждение:

Для каждого ребра простого сечения найдется цепь, проходящая только через это ребро простого сечения.

Если эта цепь идет в направлении этого ребра, то оно называется прямым, если против направления ребра, то обратным. Неориентированные ребра цепи всегда прямые.

Пропускной способностью сечения W называется сумма W(c) пропускных способностей его прямых ребер.