1. Предикат 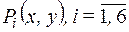 задан на множестве N2. Причем
задан на множестве N2. Причем 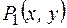 : «х > y»;
: «х > y»; 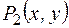 :«х < y»;
:«х < y»; 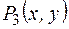 :«х
:«х 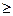 y»;
y»; 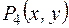 : «х
: «х 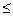 y»;
y»; 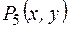 : «х делится на y без остатка»;
: «х делится на y без остатка»; 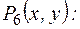 «х и y имеют общий делитель, отличный от единицы».
«х и y имеют общий делитель, отличный от единицы».
При каких 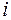 будут истинны значения предиката
будут истинны значения предиката 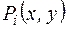 :
:
1) х = 2 и у = 4; 3) х = 5 и у = 5;
2) х = 4 и у = 2; 4) х = 7 и у = 3;
предикатного выражения:
5) 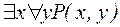 ; 7)
; 7) 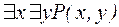 ;
;
6) 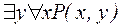 ; 8)
; 8) 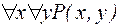 .
.
2. Указать значения выражений, которые получаются при навешивании кванторов на переменные предиката:
1) P(x, y): «x<y», заданный на множестве натуральных чисел.
2) P(x, y): «x делится на y», заданный на множестве натуральных чисел.
3) P(x, y): «x и y одновременно четные числа», заданный на множестве натуральных чисел.
4) P(x, y): «x является родителем y», заданный на множестве людей.
5) P(x, y): «x является братом y», заданный на множестве людей.
6) P(x, y): «x живет в одной квартире с y», заданный на множестве людей.
7) P(x, y): «x и y лежат на одинаковом расстоянии от начала координат», заданный на множестве точек декартовой плоскости.
8) P(x, y): «x и y лежат на одинаковом расстоянии от оси ОХ», заданный на множестве точек декартовой плоскости.
3. Пусть на множестве М= 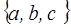 предикат P(x, y) задан таблицей.
предикат P(x, y) задан таблицей.
| х | у | Р (х, у) |
| а | а | |
| a | b | |
| a | c | |
| b | a | |
| b | b | |
| b | c | |
| c | a | |
| c | b | |
| c | c |
Навесить кванторы на его переменные всеми возможными способами и определить значения получившихся предикатных формул.
4. Проверить тождественную истинность следующих предикатных формул:
1) 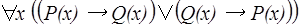 ;
;
2) 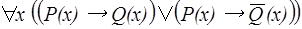 ;
;
3) 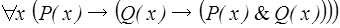 ;
;
4) 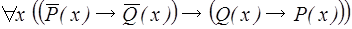 .
.
5. Получить префиксную нормальную форму следующих предикатных формул:
1) 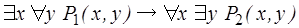 ;
;
2) 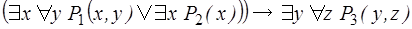 ;
;
3) 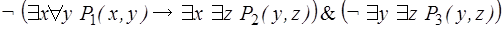 .
.
 2015-04-01
2015-04-01 510
510








