Схема вычисления функции шифрования 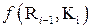 показана на рис. 5.2.
показана на рис. 5.2.
Для вычисления значения функции 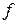 используются:
используются:
· функция 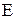 (расширение 32 бит до 48);
(расширение 32 бит до 48);
· функция 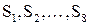 (преобразование 6‑битового числа в 4‑битовое);
(преобразование 6‑битового числа в 4‑битовое);
· функция 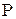 (перестановка бит в 32‑битовой последовательности).
(перестановка бит в 32‑битовой последовательности).
Приведем определения этих функций.
Аргументами функции шифрования 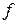 являются
являются 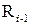 (32 бита) и
(32 бита) и 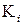 (48 бит). Результат функции
(48 бит). Результат функции 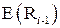 есть 48‑битовое число. Функция расширения
есть 48‑битовое число. Функция расширения 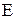 , выполняющая расширение 32 бит до 48 (принимает блок из 32 бит и порождает блок из 48 бит), определяется табл. 5.3.
, выполняющая расширение 32 бит до 48 (принимает блок из 32 бит и порождает блок из 48 бит), определяется табл. 5.3.
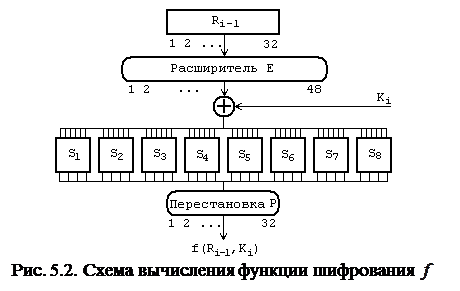 |
В соответствии с табл. 5.3 первые три бита 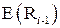 ‑ это биты 32, 1 и 2, а последние ‑ 31, 32 и 1. Полученный результат (обозначим его
‑ это биты 32, 1 и 2, а последние ‑ 31, 32 и 1. Полученный результат (обозначим его 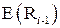 ) складывается по модулю 2 с текущим значением ключа
) складывается по модулю 2 с текущим значением ключа 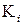 и затем разбивается на восемь 6‑битовых блоков
и затем разбивается на восемь 6‑битовых блоков 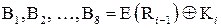 . Далее каждый из этих блоков используется как номер элемента в функциях ‑ матрицах
. Далее каждый из этих блоков используется как номер элемента в функциях ‑ матрицах 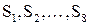 , содержащих 4‑битовые значения (табл. 5.4).
, содержащих 4‑битовые значения (табл. 5.4).
| Таблица 5.3 | |||||
| Функция E | |||||
Следует отметить, что выбор элемента в матрице 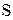 осуществляется достаточно оригинальным образом. Пусть на вход матрицы
осуществляется достаточно оригинальным образом. Пусть на вход матрицы 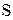 поступает 6‑битовый блок
поступает 6‑битовый блок 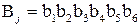 , тогда 2‑битовое число
, тогда 2‑битовое число 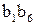 указывает номер строки матрицы, а 4‑битовое число
указывает номер строки матрицы, а 4‑битовое число 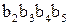 ‑ номер столбца. Например, если на вход матрицы
‑ номер столбца. Например, если на вход матрицы 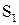 поступает 6‑битовый блок
поступает 6‑битовый блок 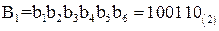 , то 2‑битовое число
, то 2‑битовое число 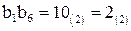 указывает строку с номером 2 матрицы
указывает строку с номером 2 матрицы 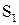 , а 4‑битовое число
, а 4‑битовое число 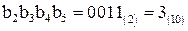 указывает столбец с номером 3 матрицы
указывает столбец с номером 3 матрицы 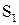 . Это означает, что в матрице
. Это означает, что в матрице 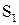 блок
блок 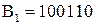 выбирает элемент на пересечении строки с номером 2 и столбца с номером 3, т.е. элемент
выбирает элемент на пересечении строки с номером 2 и столбца с номером 3, т.е. элемент 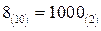 . Совокупность 6‑битовых блоков
. Совокупность 6‑битовых блоков 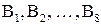 обеспечивает выбор 4-битового элемента в каждой из матриц
обеспечивает выбор 4-битового элемента в каждой из матриц 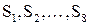 .
.
| Таблица 5.4 | |||||||||||||||||
| Функции S | |||||||||||||||||
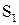
| |||||||||||||||||
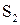
| |||||||||||||||||
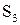
| |||||||||||||||||
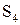
| |||||||||||||||||
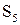
| |||||||||||||||||
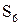
| |||||||||||||||||
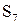
| |||||||||||||||||
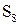
| |||||||||||||||||
В результате получаем 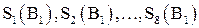 , т.е. 32‑битовый блок (поскольку матрицы
, т.е. 32‑битовый блок (поскольку матрицы 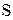 , содержат 4‑битовые элементы). Этот 32‑битовый блок преобразуется с помощью функции перестановки бит
, содержат 4‑битовые элементы). Этот 32‑битовый блок преобразуется с помощью функции перестановки бит 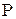 (табл. 5.5).
(табл. 5.5).
| Таблица 5.5 | |||
| Функция P | |||
Таким образом, функция шифрования
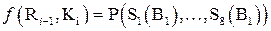 .
.
 2015-04-01
2015-04-01 624
624








