В модулярной арифметике все арифметические действия выполняются как в обычной арифметике с учетом того, что получаемые числа не могут превышать некоторой величины называемой модулем.
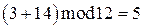
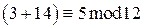
В общем случае 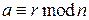 . Читается
. Читается 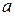 сравнимо с
сравнимо с 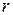 по модулю
по модулю 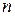 . Это справедливо, если
. Это справедливо, если 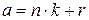 , где
, где 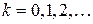 . Отсюда
. Отсюда 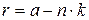 называется вычетом числа
называется вычетом числа 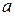 по модулю
по модулю 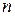 ,
, 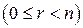 . Справедливо:
. Справедливо:
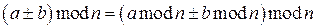 ;
;
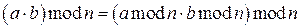 ;
;
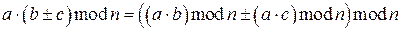 .
.
Использование модулярной арифметики позволяет оперировать с очень большими числами, например, при возведении в степень:
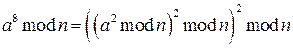 .
.
Малая теорема Ферма
Если 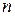 ‑ простое и
‑ простое и 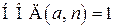 , то
, то
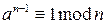 .
.
 2015-04-01
2015-04-01 444
444








