Количество положительных целых, меньших 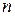 , которые взаимно просты с
, которые взаимно просты с 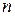 , определяется с помощью функции Эйлера
, определяется с помощью функции Эйлера 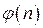 :
:
| Модуль | 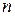 простое простое
| 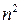
| 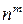
| 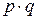 ( (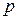 и и 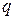 простые) простые)
|
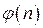
| 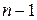
| 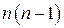
| 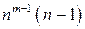
| 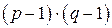
|
Обобщение Эйлера малой теоремы Ферма: если 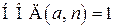 , то
, то
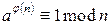 .
.
Нахождение обратных величин
Если задано уравнение 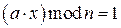 , то величина
, то величина 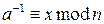 называется обратной величиной
называется обратной величиной 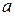 по модулю
по модулю 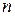 .
.
Обратная величина существует, если 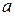 и
и 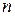 – взаимно простые числа.
– взаимно простые числа.
Способы нахождения обратных чисел
1. Перебором возможных значений.
Подставляя вместо 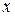 числа:
числа: 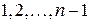 – добиваемся выполнения исходного уравнения.
– добиваемся выполнения исходного уравнения.
Пример 6.1. 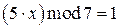 ,
, 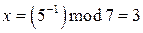 , т.к.
, т.к. 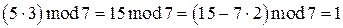 .
.
2. С помощью функции Эйлера 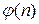 .
.
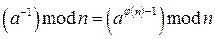 .
.
 2015-04-01
2015-04-01 639
639








